题目内容
(本题满分15分)设M是由满足下列条件的函数![]() 构成的集合:“①方程
构成的集合:“①方程![]() 有实数根;②函数
有实数根;②函数![]() 的导数
的导数![]() 满足
满足![]() ”
”
(I)证明:函数![]() 是集合M中的元素;
是集合M中的元素;
(II)证明:函数![]() 具有下面的性质:对于任意
具有下面的性质:对于任意![]()
![]() ,都存在
,都存在![]() ,使得等式
,使得等式![]() 成立。
成立。
(III)若集合M中的元素![]() 具有下面的性质:若
具有下面的性质:若![]() 的定义域为D,则对于任意[m,n]
的定义域为D,则对于任意[m,n]![]() ,都存在
,都存在![]() ,使得等式
,使得等式![]() 成立。试用这一性质证明:对集合M中的任一元素
成立。试用这一性质证明:对集合M中的任一元素![]() ,方程
,方程![]() 只有一个实数根。
只有一个实数根。
(Ⅰ) 见解析 (Ⅱ) 见解析 (Ⅲ)见解析
解析:
(I)证明:因为![]() ,又因为当x=0时,
,又因为当x=0时,![]() ,所以方程
,所以方程![]() 有实数根0。
有实数根0。
所以函数![]() 是集合M中的元素。 ………………4分
是集合M中的元素。 ………………4分
(II)证明: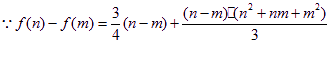 ,
,![]()
![]() [m,n]
[m,n]![]()
![]() 。
。
又,![]() 。
。
![]()
![]() 也就是
也就是![]() ;
;
………………9分
(III)假设方程f(x)-x=0存在两个实数根![]() 不妨设
不妨设![]() ,根据题意存在数
,根据题意存在数![]()
使得等式![]() 成立。
成立。
因为![]()
与已知![]() 矛盾,所以方程
矛盾,所以方程![]() 只有一个实数根。……15分
只有一个实数根。……15分

练习册系列答案
相关题目
 .
. 在
在 上单调递增,在
上单调递增,在 上单调递减,求实数
上单调递减,求实数 的最大值;
的最大值; 对任意的
对任意的 ,
, 都成立,求实数
都成立,求实数 的取值范围.
的取值范围. 为自然对数的底数.
为自然对数的底数.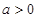 ,函数
,函数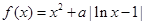 .
. 时,求函数
时,求函数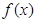 的单调增区间;
的单调增区间; 时,不等式
时,不等式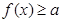 恒成立,实数
恒成立,实数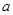 的取值范围.
的取值范围.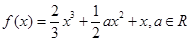 .
.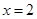 时,
时,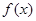 取得极值,求
取得极值,求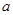 的值;
的值;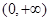 内为增函数,求
内为增函数,求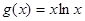 ,是否存在正实数
,是否存在正实数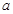 ,使得对任意
,使得对任意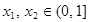 ,都有
,都有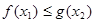 成立?
成立?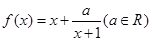 .
.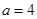 时,解不等式:
时,解不等式: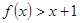 ;
; 在
在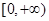 的最小值;
的最小值;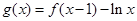 的单调递增区间.
的单调递增区间.