题目内容
(本题满分15分)设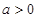 ,函数
,函数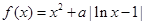 .
.
(Ⅰ)当 时,求函数
时,求函数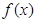 的单调增区间;
的单调增区间;
(Ⅱ)若 时,不等式
时,不等式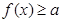 恒成立,实数
恒成立,实数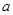 的取值范围.
的取值范围.
【答案】
解:(Ⅰ)当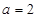 时,
时,

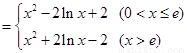 ………2分
………2分
当 时,
时,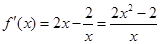 ,
,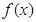 在
在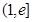 内单调递增;
内单调递增;
当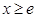 时,
时, 恒成立,故
恒成立,故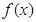 在
在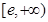 内单调递增;
内单调递增;
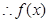 的单调增区间为
的单调增区间为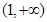 。
…………6分
。
…………6分
(Ⅱ)①当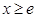 时,
时,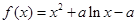 ,
,
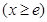
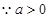 ,
,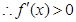 恒成立,
恒成立,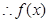 在
在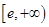 上增函数。
上增函数。
故当 时,
时,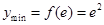 。
…………8分
。
…………8分
②当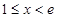 时,
时,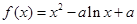 ,
,
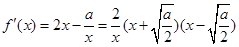
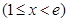
(Ⅰ)当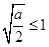 ,即
,即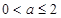 时,
时,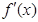 在
在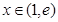 时为正数,所以
时为正数,所以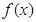 在区间
在区间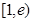 上为增函数。故当
上为增函数。故当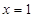 时,
时, ,且此时
,且此时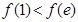 …………10分
…………10分
(Ⅱ)当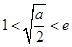 ,即
,即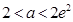 时,
时,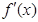 在
在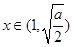 时为负数,在
时为负数,在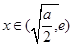 时为正数,所以
时为正数,所以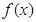 在区间
在区间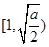 上为减函数,在
上为减函数,在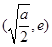 上为增函数。故当
上为增函数。故当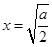 时,
时,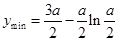 ,且此时
,且此时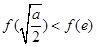 。
…………12分
。
…………12分
(Ⅲ)当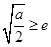 ,即
,即 时,
时,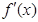 在
在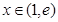 进为负数,所以
进为负数,所以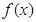 在区间
在区间 上为减函数,故当
上为减函数,故当 时,
时,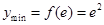 。
…………14分
。
…………14分
所以函数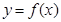 的最小值为
的最小值为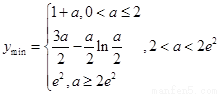 。
。
由条件得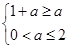 此时
此时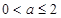 ;或
;或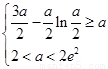 ,此时
,此时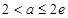 ;或
;或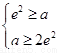 ,此时无解。
,此时无解。
综上,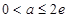 。
…………15分
。
…………15分
【解析】略

练习册系列答案
相关题目
 .
. 在
在 上单调递增,在
上单调递增,在 上单调递减,求实数
上单调递减,求实数 的最大值;
的最大值; 对任意的
对任意的 ,
, 都成立,求实数
都成立,求实数 的取值范围.
的取值范围. 为自然对数的底数.
为自然对数的底数.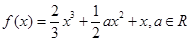 .
.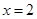 时,
时,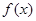 取得极值,求
取得极值,求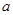 的值;
的值;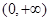 内为增函数,求
内为增函数,求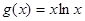 ,是否存在正实数
,是否存在正实数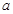 ,使得对任意
,使得对任意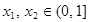 ,都有
,都有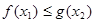 成立?
成立?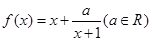 .
.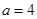 时,解不等式:
时,解不等式: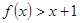 ;
;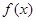 在
在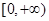 的最小值;
的最小值;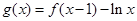 的单调递增区间.
的单调递增区间.