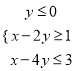题目内容
【题目】如图1:已知正方形ABCD的边长是2,有一动点M从点B出发沿正方形的边运动,路线是B→C→D→A.设点M经过的路程为x,△ABM的面积为S. 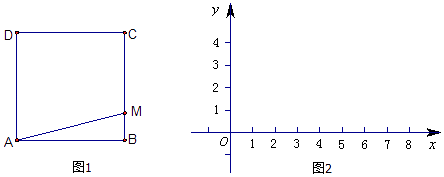
(1)求函数S=f(x)的解析式及其定义域;
(2)在图2中画出函数S=f(x)的图象.
【答案】
(1)解:由题意,当M从B到C时, ![]() =x,(0≤x≤2)
=x,(0≤x≤2)
当M从C到D时,S△ABM= ![]() ABBC=2(2<x≤4),
ABBC=2(2<x≤4),
当M从D到A时,S△ABM= ![]() AB(6﹣x)=6﹣x(4<x≤6),
AB(6﹣x)=6﹣x(4<x≤6),
函数S=f(x)= 
其定义域为{x|0≤x≤6}
(2)解:由(1)的解析式可得:当0≤x≤2时,f(x)=x,值域为[0,2],
当2<x≤4时,f(x)=2,值域为{2}
当4<x≤6时,f(x)=6﹣x,值域为[0,2).
故图象如下:

【解析】(1)由题意,当M从B到C过程,三角形ABM的面积为S随x的增大而增大,当M从C到D过程,三角形ABM的面积为S随x的增大而不变,当M从D到A过程,三角形ABM的面积为S随x的增大而减小.分段函数,可得解析式及其定义域.(2)根据(1)的函数关系式,求值域,作图即可.

练习册系列答案
相关题目