题目内容
16.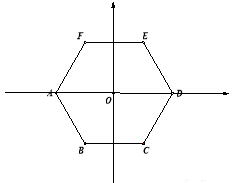 已知正六边形ABCDEF的边长是2,以正六边形中心为原点,以对角线AD所在的直线为x轴,如图建立平面直角坐标系.
已知正六边形ABCDEF的边长是2,以正六边形中心为原点,以对角线AD所在的直线为x轴,如图建立平面直角坐标系.(1)求边AF所在的直线的方程;
(2)求过点P(1,0),且与AB边所在直线垂直的直线的方程.
分析 (1)求出A、F的坐标,用两点式写出AF边所在的直线方程,并化为一般式.
(2)求出B点的坐标,求出kAB,再根据直线垂直的条件求出所求直线的斜率,利用点斜式即可求出.
解答 解:(1)由题意知A(-2,0),F(-1,$\sqrt{3}$),用两点式写出AF边所在的直线方程$\frac{y-0}{0-\sqrt{3}}$=$\frac{x+2}{-2-(-1)}$,
即$\sqrt{3}$x-y+2$\sqrt{3}$=0,
(2)由题意知B(-1,-$\sqrt{3}$),
∴kAB=$\frac{-\sqrt{3}-0}{-1-(-2)}$=-$\frac{\sqrt{3}}{2}$,
设与AB边所在直线垂直的直线的方程的斜率为k,
则-$\frac{\sqrt{3}}{2}$k=-1,解得k=$\frac{2\sqrt{3}}{3}$,
∴点P(1,0),且与AB边所在直线垂直的直线的方程y-0=$\frac{2\sqrt{3}}{3}$(x-1),即2$\sqrt{3}$x-3y-2$\sqrt{3}$=0.
点评 本题考查用两点式求直线的方程的方法,斜率的确定方法,体现了数形结合的数学思想.

练习册系列答案
 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案
相关题目
6.x∈R,y=5-sin$\frac{x}{2}$的最大值是( )
| A. | 3 | B. | 4 | C. | 5 | D. | 6 |