Question

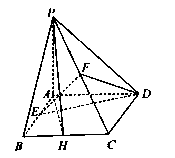
【题目】如图，在直角梯形 中， ， ， ， 为线段 的中点，将 沿 折起，使平面 平面 ，得到几何体 .

（1）若 分别为线段 的中点，求证： 平面 ；
（2）求证： 平面 ；
（3）求 的值.

Answer 1

【答案】
（1）证明：∵折叠前后CD、BG位置关系不改变，
∴CD∥BG．
∵ E、F分别为线段AC、BD的中点，
∴EF∥CD，
∴ EF∥BG．
又EF 平面ABG，BG平面ABG，
∴ EF∥平面ABG．

（2）证明：∵ 将△ADG沿GD折起后，AG、GD位置关系不改变，
∴AG⊥GD，
又平面ADG⊥平面BCDG，平面ADG∩平面BCDG＝GD，AG平面AGD，
∴ AG⊥平面BCDG
（3）由已知得BC＝CD＝AG＝2，
又由(2)得AG⊥平面BCDG，
∴点A到平面BCDG的距离AG＝2，
∴
【解析】（1）根据中位线定理证明EF//CD，再根据直线与直线平行的性质证明EF//GB，最后根据直线与平面平行的判定定理，证明 EF//平面ABG。
（2）根据平面与平面垂直的性质定理可以证明结论。
（3）利用等体积法，结合三棱锥的体积计算公式求解。