题目内容
（2013•莱芜二模）已知m，n是两条不同直线，α，β是两个不同平面，给出四个命题：
①若α∩β=m，n?α，n⊥m，则α⊥β
②若m⊥α，m⊥β，则α∥β
③若m⊥α，n⊥β，m⊥n，则α⊥β
④若m∥α，n∥βm∥n，则α∥β
其中正确的命题是（ ）
①若α∩β=m，n?α，n⊥m，则α⊥β
②若m⊥α，m⊥β，则α∥β
③若m⊥α，n⊥β，m⊥n，则α⊥β
④若m∥α，n∥βm∥n，则α∥β
其中正确的命题是（ ）
分析：由面面垂直的判定定理，可判断①的真假；由面面平行的判定定理及线面垂直的几何特征，可以判断②的真假；由面面垂直的判定定理，及线面垂直的几何特征，可以判断③的真假；根据线面平行的几何特征及面面平行的判定方法，可以判断④的真假．
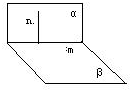
解答：解：①若α∩β=m，n?α，n⊥m，如图，则α与β不一定垂直，故①为假命题；
②若m⊥α，m⊥β，根据垂直于同一条直线的两个平面平行，则α∥β；故②为真命题；
③若m⊥α，n⊥β，m⊥n，则α⊥β，故③为真命题；
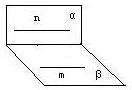
④若m∥α，n∥β，m∥n，如图，则α与β可能相交，故④为假命题．
故选B．
②若m⊥α，m⊥β，根据垂直于同一条直线的两个平面平行，则α∥β；故②为真命题；
③若m⊥α，n⊥β，m⊥n，则α⊥β，故③为真命题；
④若m∥α，n∥β，m∥n，如图，则α与β可能相交，故④为假命题．
故选B．
点评：本题考查的知识点是平面与平面之间的位置关系，熟练掌握空间直线与平面平行及垂直的判定定理、性质定义、几何特征是解答的关键．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目