题目内容
求1+2+3+…+n的值（不利用求和公式）．
考点：数列的求和
专题：等差数列与等比数列
分析：利用“倒序相加法”即可得出．
解答：
解：Sn=1+2+3+…+n，
∴2Sn=（1+n）+（2+n-1）+…+（n+1）=n（n+1），
∴Sn=
．
∴2Sn=（1+n）+（2+n-1）+…+（n+1）=n（n+1），
∴Sn=
| n(n+1) |
| 2 |
点评：本题考查了等差数列的“倒序相加法”，属于基础题．
练习册系列答案
金牌课堂练系列答案
三新快车金牌周周练系列答案
相关题目
函数f（x）=（
sinx-cosx）cosx的值域是（ ）
| 3 |
A、[-
| ||||
B、[-
| ||||
C、[-
| ||||
D、[-
|
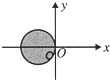
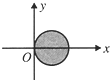
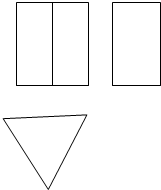如图所示是一个几何体的三视图，若其正视图的面积为4cm2，俯视图的面积为下列函数中，在（0，+∞）上单调递减的函数是（ ）
| A、y=（x-1）2 | ||
B、y=
| ||
| C、y=ex | ||
| D、y=ln（x+1） |