题目内容
若函数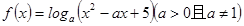 满足对任意的
满足对任意的 ,当
,当 时
时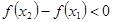 ,则实数
,则实数 的取值范围是( )
的取值范围是( )
A. | B.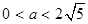 | C.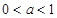 | D.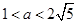 |
C
解析试题分析:当 时
时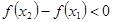 ,说明函数在
,说明函数在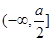 上是减函数,根据复合函数的单调性的性质,有
上是减函数,根据复合函数的单调性的性质,有

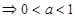 .
.
考点:复合函数的单调性.

练习册系列答案
相关题目
若函数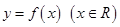 满足
满足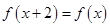 且
且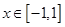 时,
时,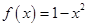 ,函数
,函数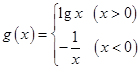 ,则函数
,则函数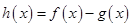 在区间
在区间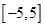 内的零点的个数为( )
内的零点的个数为( )
A.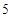 | B.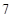 | C.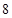 | D.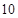 |
已知偶函数 在区间
在区间 单调增加,则满足
单调增加,则满足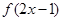 <
<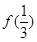 的
的 取值范围是( )
取值范围是( )
A.(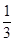 , ,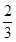 ) ) | B.[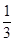 , ,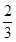 ) ) | C.(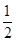 , ,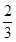 ) ) | D.[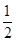 , ,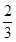 ) ) |
已知函数f(x)在R上为奇函数,对任意的 ,总有
,总有 且
且 ,则不等式
,则不等式 <0的解集为 ( )
<0的解集为 ( )
| A.(-1,0)∪(1,+∞) | B.(-∞,-1)∪(0,1) |
| C.(-∞,-1)∪(1,+∞) | D.(-1,0)∪(0,1) |
如图是函数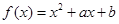 的部分图像,函数
的部分图像,函数 的零点所在的区间是
的零点所在的区间是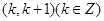 ,则
,则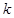 的值为( )
的值为( )
A. 1或0 1或0 | B.0 | C. 1或1 1或1 | D.0或1 |
若函数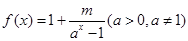 是奇函数,则
是奇函数,则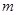 为
为
A.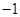 | B.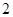 | C.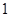 | D.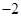 |
下列四组函数中,其函数图象相同的是 ( ).
A.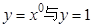 | B.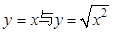 |
C.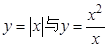 | D.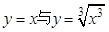 |
函数 的定义域为( ).
的定义域为( ).
A. | B. | C. | D. |
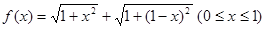 的性质,构造了如图所示的两个边长为
的性质,构造了如图所示的两个边长为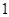 的正方形
的正方形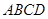 和
和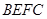 ,点
,点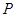 是边
是边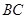 上的一个动点,设
上的一个动点,设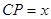 ,则
,则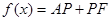 .那么可推知方程
.那么可推知方程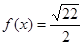 解的个数是( )
解的个数是( )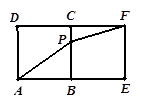
 .
.  .
.  .
.