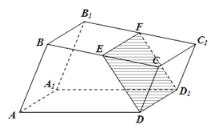
题目内容
【题目】已知四棱锥![]() 中,底面
中,底面![]() 为平行四边形,点
为平行四边形,点![]() 、
、![]() 、
、![]() 分别在
分别在![]() 、
、![]() 、
、![]() 上.
上.

(1)若![]() ,求证:平面
,求证:平面![]() 平面
平面![]() ;
;
(2)若![]() 满足
满足![]() ,则
,则![]() 点满足什么条件时,
点满足什么条件时,![]() 面
面![]() .
.
【答案】(1)证明见解析;(2)当点![]() 是
是![]() 的中点时,
的中点时,![]() 面
面![]() .
.
【解析】
(1)由![]() 可证明出
可证明出![]() ,再由
,再由![]() ,可得出
,可得出![]() ,利用直线与平面平行的判定定理可证明出
,利用直线与平面平行的判定定理可证明出![]() 平面
平面![]() ,同理证明
,同理证明![]() 平面
平面![]() ,再由平面与平面平行的判定定理可证明出平面
,再由平面与平面平行的判定定理可证明出平面![]() 平面
平面![]() ;
;
(2)连接![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() ,取
,取![]() 的中点
的中点![]() ,取
,取![]() 的中点
的中点![]() ,连接
,连接![]() 、
、![]() 、
、![]() ,利用直线与平面平行的判定定理证明出
,利用直线与平面平行的判定定理证明出![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,再利用平面与平面平行的判定定理证明出平面
,再利用平面与平面平行的判定定理证明出平面![]() 平面
平面![]() ,于此可得出
,于此可得出![]() 平面
平面![]() .
.
(1)![]() ,
,![]() ,
,
![]() 四边形
四边形![]() 是平行四边形,
是平行四边形,![]() ,
,![]() ,
,
![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,![]() 平面
平面![]() .
.
又![]() ,
,![]() ,
,
![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,![]() 平面
平面![]() .
.
![]() ,
,![]() 、
、![]() 平面
平面![]() ,
,![]() 平面
平面![]() 平面
平面![]() ;
;
(2)连接![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() ,取
,取![]() 的中点
的中点![]() ,取
,取![]() 的中点
的中点![]() ,连接
,连接![]() 、
、![]() 、
、![]() ,则点
,则点![]() 为
为![]() 的中点,下面证明:当点
的中点,下面证明:当点![]() 为
为![]() 的中点时,
的中点时,![]() 平面
平面![]() .
.

![]() 且
且![]() 为
为![]() 的中点,
的中点,![]() ,
,![]() 为
为![]() 的中点,
的中点,
又![]() 点
点![]() 为
为![]() 的中点,
的中点,![]() ,
,
![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,同理,
,同理,![]() 平面
平面![]() .
.
![]() ,
,![]() 、
、![]() 平面
平面![]() ,
,![]() 平面
平面![]() 平面
平面![]() .
.
![]() 平面
平面![]() ,
,![]() 平面
平面![]() .
.
因此,当点![]() 是
是![]() 的中点时,
的中点时,![]() 面
面![]() .
.

练习册系列答案
 黎明文化寒假作业系列答案
黎明文化寒假作业系列答案
相关题目
【题目】某电视台问政直播节目首场内容是“让交通更顺畅”.A、B、C、D四个管理部门的负责人接受问政,分别负责问政A、B、C、D四个管理部门的现场市民代表(每一名代表只参加一个部门的问政)人数的条形图如下.为了了解市民对武汉市实施“让交通更顺畅”几个月来的评价,对每位现场市民都进行了问卷调查,然后用分层抽样的方法从调查问卷中抽取20份进行统计,统计结果如下面表格所示:
满意 | 一般 | 不满意 | |
A部门 | 50% | 25% | 25% |
B部门 | 80% | 0 | 20% |
C部门 | 50% | 50% | 0 |
D部门 | 40% | 20% | 40% |

(1)若市民甲选择的是A部门,求甲的调查问卷被选中的概率;
(2)若想从调查问卷被选中且填写不满意的市民中再选出2人进行电视访谈,求这两人中至少有一人选择的是D部门的概率.