题目内容
【题目】如图,已知直四棱柱![]() 的底面是直角梯形,
的底面是直角梯形,![]() ,
,![]() ,
,![]() 、
、![]() 分别是棱
分别是棱![]() 、
、![]() 上的动点,且
上的动点,且![]() ,
,![]() ,
,![]() ,
,![]() .
.
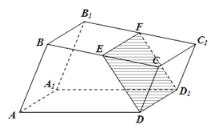
(1)证明:无论点![]() 怎样运动,四边形
怎样运动,四边形![]() 都为矩形;
都为矩形;
(2)当![]() 时,求几何体
时,求几何体![]() 的体积.
的体积.
【答案】(1)证明见解析;(2)![]() .
.
【解析】
(1)利用面面平行的性质定理得出![]() ,由面面平行的性质定理可得出
,由面面平行的性质定理可得出![]() ,可证明出四边形
,可证明出四边形![]() 为平行四边形,由
为平行四边形,由![]() 平面
平面![]() ,可得出
,可得出![]() ,从而可证明出四边形
,从而可证明出四边形![]() 为矩形;
为矩形;
(2)计算出梯形![]() 的面积和
的面积和![]() 的面积,将梯形
的面积,将梯形![]() 的面积减去
的面积减去![]() 的面积可得出四边形
的面积可得出四边形![]() 的面积,再利用柱体的体积公式可求出几何体
的面积,再利用柱体的体积公式可求出几何体![]() 的体积.
的体积.
(1)在直四棱柱![]() 中,
中,![]() ,
,![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() ,
,![]() .
.
在直四棱柱![]() 中,平面
中,平面![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() ,
,![]() ,则四边形
,则四边形![]() 为平行四边形,
为平行四边形,
在直四棱柱![]() 中,
中,![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,![]() ,
,
因此,无论点![]() 怎样运动,四边形
怎样运动,四边形![]() 都为矩形;
都为矩形;
(2)由于四边形![]() 是直角梯形,且
是直角梯形,且![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
所以,梯形![]() 的面积为
的面积为![]() ,
,
![]() ,易得
,易得![]() ,
,![]() 的面积为
的面积为![]() ,
,
![]() 四边形
四边形![]() 的面积为
的面积为![]() ,
,
由题意可知,几何体![]() 为直四棱柱,且高为
为直四棱柱,且高为![]() ,
,
因此,几何体![]() 的体积为
的体积为![]() .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
【题目】为了鼓励节约用电,辽宁省实行阶梯电价制度,其中每户的用电单价与户年用电量的关系如下表所示.
分档 | 户年用电量(度) | 用电单价(元/度) |
第一阶梯 |
| 0.5 |
第二阶梯 |
| 0.55 |
第三阶梯 |
| 0.80 |
记用户年用电量为![]() 度时应缴纳的电费为
度时应缴纳的电费为![]() 元.
元.
(1)写出![]() 的解析式;
的解析式;
(2)假设居住在沈阳的范伟一家2018年共用电3000度,则范伟一家2018年应缴纳电费多少元?
(3)居住在大连的张莉一家在2018年共缴纳电费1942元,则张莉一家在2018年用了多少度电?