题目内容
设函数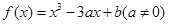 .
.
(Ⅰ)若曲线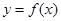 在点
在点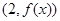 处与直线
处与直线 相切,求
相切,求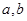 的值;
的值;
(Ⅱ)求函数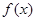 的单调区间与极值点.
的单调区间与极值点.
(1)a=4,b=24
(2) 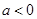 时,
时,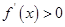 ,函数
,函数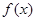 在
在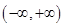 上单调递增,
上单调递增,
此时函数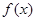 没有极值点
没有极值点
当 时,由
时,由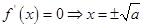 ,
,
当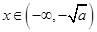 时,
时,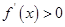 ,函数
,函数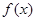 单调递增,
单调递增,
当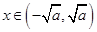 时,
时,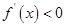 ,函数
,函数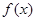 单调递减,
单调递减,
当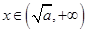 时,
时,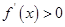 ,函数
,函数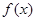 单调递增,
单调递增,
∴此时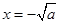 是
是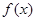 的极大值点,
的极大值点,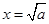 是
是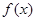 的极小值点
的极小值点
解析试题分析:解:(Ⅰ)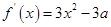 , 2分
, 2分
∵曲线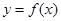 在点
在点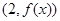 处与直线
处与直线 相切,
相切,
∴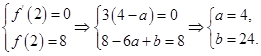 6分
6分
(Ⅱ)∵ ,
,
当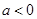 时,
时,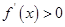 ,函数
,函数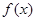 在
在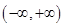 上单调递增,
上单调递增,
此时函数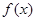 没有极值点 8分
没有极值点 8分
当 时,由
时,由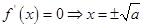 , 9分
, 9分
当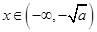 时,
时,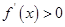 ,函数
,函数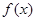 单调递增, 10分
单调递增, 10分
当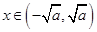 时,
时,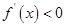 ,函数
,函数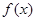 单调递减, 11分
单调递减, 11分
当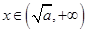 时,
时,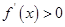 ,函数
,函数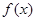 单调递增, 12分
单调递增, 12分
∴此时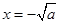 是
是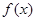 的极大值点, 13分
的极大值点, 13分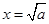 是
是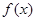 的极小值点 14分
的极小值点 14分
考点:导数的几何意义和函数的极值
点评:主要是考查了运用导数求解切线方程和极值问题,属于基础题。

练习册系列答案
相关题目
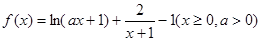 。
。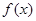 在
在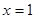 处取得极值,求
处取得极值,求 的值;
的值;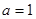 且
且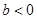 ,函数
,函数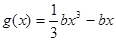 ,若对于
,若对于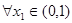 ,总存在
,总存在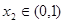 使得
使得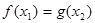 ,求实数
,求实数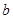 的取值范围。
的取值范围。 为实数,
为实数, ,
, ,求
,求 的单调区间;
的单调区间; ,求
,求 的函数
的函数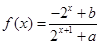 是奇函数。
是奇函数。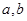 的值;
的值;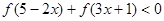
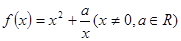
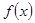 的奇偶性;
的奇偶性;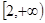 是增函数,求实数
是增函数,求实数 的取值范围。
的取值范围。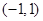 上的函数
上的函数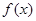 满足:①对任意
满足:①对任意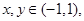 都有
都有 ;
;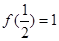 .
.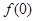 的值;
的值;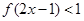 .
.
 的最小正周期.
的最小正周期. 时,求函数
时,求函数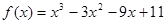
 的递减区间;
的递减区间;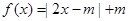 .
. 的解集为
的解集为 ,求实数
,求实数 的值;
的值;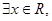 使
使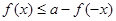 能成立,求实数a的取值范围.
能成立,求实数a的取值范围.