题目内容
【题目】设圆![]() 的圆心为
的圆心为![]() ,直线
,直线![]() 过点
过点![]() 且与
且与![]() 轴不重合,交圆
轴不重合,交圆![]() 于
于![]() ,
,![]() 两点,过点
两点,过点![]() 作
作![]() 的平行线交
的平行线交![]() 于点
于点![]() .
.
(1)求![]() 的值;
的值;
(2)设点![]() 的轨迹为曲线
的轨迹为曲线![]() ,直线
,直线![]() 与曲线
与曲线![]() 相交于
相交于![]() ,
,![]() 两点,与直线
两点,与直线![]() 相交于
相交于![]() 点,试问在椭圆
点,试问在椭圆![]() 上是否存在一定点
上是否存在一定点![]() ,使得
,使得![]() ,
,![]() ,
,![]() 成等差数列(其中
成等差数列(其中![]() ,
,![]() ,
,![]() 分别指直线
分别指直线![]() ,
,![]() ,
,![]() 的斜率).若存在,求出
的斜率).若存在,求出![]() 点的坐标;若不存在,请说明理由.
点的坐标;若不存在,请说明理由.
【答案】(1) ![]() (2)见证明
(2)见证明
【解析】
(1)由![]() 且
且![]() ,可得
,可得![]() ,进而得到
,进而得到![]()
![]() ,再由半径
,再由半径![]() ,即可求解;
,即可求解;
(2)由(1)知得![]() 的方程,设直线
的方程,设直线![]() 的方程为
的方程为![]() ,代入椭圆的方程,利用根与系数的关系和
,代入椭圆的方程,利用根与系数的关系和![]() ,
,![]() ,
,![]() 成等差数列,求得
成等差数列,求得![]()
![]() ,由对任意的
,由对任意的![]() 该等式恒成立,求得
该等式恒成立,求得![]() ,即可得到答案.
,即可得到答案.
(1)因为圆![]() 的圆心为
的圆心为![]() ,所以
,所以![]() 且
且![]() ,
,
所以![]() ,所以
,所以![]() ,
,
所以![]() ,
,
又因为圆![]() 的半径为8,即
的半径为8,即![]() ,
,
所以![]() .
.
(2)由(1)知,曲线![]() 是以
是以![]() ,
,![]() 为焦点的椭圆,且长轴长为8,
为焦点的椭圆,且长轴长为8,
所以曲线![]() 的方程为
的方程为![]() ,
,
设直线![]() 的方程为
的方程为![]() ,
,
代入椭圆化简得![]() ,
,
设![]() ,
,![]() ,
,![]() ,则
,则![]() ,
,![]() ,
,
所以![]()
![]()
 ,
,
因为![]() ,
,![]() ,
,![]() 成等差数列,所以
成等差数列,所以![]() ,
,
因为![]() ,所以
,所以![]()
 ,
,
化简得![]() ,
,
对任意的![]() 该等式恒成立,所以
该等式恒成立,所以![]() ,
,
所以存在点![]() ,使得
,使得![]() ,
,![]() ,
,![]() 成等差数列.
成等差数列.

练习册系列答案
相关题目
【题目】某歌手大赛进行电视直播,比赛现场有6名特约嘉宾给每位参赛选手评分,场内外的观众可以通过网络平台给每位参赛选手评分.某选手参加比赛后,现场嘉宾评分情况如下表;场内外共有数万名观众参与了评分,组织方将观众评分按照![]() ,
,![]() ,
,![]() 分组,绘成频率分布直方图如下:
分组,绘成频率分布直方图如下:
嘉宾 |
|
|
|
|
|
|
评分 | 96 | 95 | 96 | 89 | 97 | 98 |
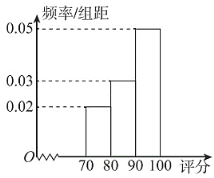
(1)从观众中任取三人,求这三人中恰有1人分数在![]() 另2人分数在
另2人分数在![]() 的概率;
的概率;
(2)从嘉宾中随机选3人,记3人中分数不低于96分的人数为![]() ,求
,求![]() 的期望;
的期望;
(3)嘉宾评分的平均数为![]() ,场内外的观众评分的平均数为
,场内外的观众评分的平均数为![]() 与
与![]() 的大小关系(不需要证明).
的大小关系(不需要证明).