题目内容
设函数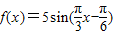 ,若对任意x∈R,都有f(x1)≤f(x)≤f(x2)成立,则|x1-x2|的最小值为 .
,若对任意x∈R,都有f(x1)≤f(x)≤f(x2)成立,则|x1-x2|的最小值为 .
【答案】分析:根据题意,x1、x2是函数的两个最值点,一个是最小值点且另一个是最大值点.由此可得|x1-x2|=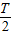 •(2k-1),(k∈N*),利用三角函数的周期公式即可算出|x1-x2|的最小值.
•(2k-1),(k∈N*),利用三角函数的周期公式即可算出|x1-x2|的最小值.
解答:解:∵对任意x∈R,都有f(x1)≤f(x)≤f(x2)成立,
∴x1、x2是函数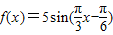 的两个最值点,其中一个是最小值点,另一个是最大值点
的两个最值点,其中一个是最小值点,另一个是最大值点
因此,|x1-x2|等于半个周期的正奇数倍
∵函数的周期T=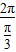 =6
=6
∴|x1-x2|=3(2k-1),(k∈N*),取k=1,得|x1-x2|的最小值为3.
故答案为:3
点评:本题给出函数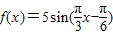 满足的条件,求|x1-x2|的最小值.着重考查了三角函数的周期公式、正弦函数的图象与性质等知识,属于基础题.
满足的条件,求|x1-x2|的最小值.着重考查了三角函数的周期公式、正弦函数的图象与性质等知识,属于基础题.
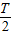 •(2k-1),(k∈N*),利用三角函数的周期公式即可算出|x1-x2|的最小值.
•(2k-1),(k∈N*),利用三角函数的周期公式即可算出|x1-x2|的最小值.解答:解:∵对任意x∈R,都有f(x1)≤f(x)≤f(x2)成立,
∴x1、x2是函数
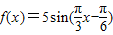 的两个最值点,其中一个是最小值点,另一个是最大值点
的两个最值点,其中一个是最小值点,另一个是最大值点因此,|x1-x2|等于半个周期的正奇数倍
∵函数的周期T=
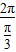 =6
=6∴|x1-x2|=3(2k-1),(k∈N*),取k=1,得|x1-x2|的最小值为3.
故答案为:3
点评:本题给出函数
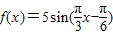 满足的条件,求|x1-x2|的最小值.着重考查了三角函数的周期公式、正弦函数的图象与性质等知识,属于基础题.
满足的条件,求|x1-x2|的最小值.着重考查了三角函数的周期公式、正弦函数的图象与性质等知识,属于基础题. 
练习册系列答案
 学练快车道快乐假期寒假作业系列答案
学练快车道快乐假期寒假作业系列答案
相关题目
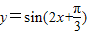 ,若对任意x∈R,存在x1,x2使f(x1)≤f(x)≤f(x2)恒成立,则|x1-x2|的最小值是 .
,若对任意x∈R,存在x1,x2使f(x1)≤f(x)≤f(x2)恒成立,则|x1-x2|的最小值是 .