题目内容
对同一目标进行两次射击,第一、二次射击命中目标的概率分别为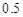 和
和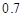 ,则两次射击中至少有一次命中目标的概率是( )
,则两次射击中至少有一次命中目标的概率是( )
A.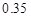 | B.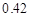 | C.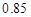 | D.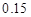 |
C
解析试题分析:由题意可得两人没有击中目标的概率,根据题意可得两人是否击中目标是相互独立的,然后根据相互独立事件的概率乘法公式可得答案.解:由题意可得:两人是否击中目标是相互独立的,因为两人击中目标的概率分别是0.5和0.7,所以两人没有击中目标的概率分别是0.5和0.3,所以两人都没有击中目标的概率为:0.5×0.3=0.15.根据对立事件的概率公式可知,那么两次射击中至少有一次命中目标的概率是1—0.15=0.85,故选C.
考点:相互独立事件
点评:本题主要考查相互独立事件的定义与相互独立事件的概率乘法公式的应用,此题属于基础题,只要学生认知细心的计算即可得到全分.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
公务员考试分笔试和面试,笔试的通过率为20%,最后的录取率为4%,已知某人已经通过笔试,则他最后被录取的概率为( )
| A.20% | B.24% | C.16% | D.4% |
一射手对同一目标独立地射击四次,已知至少命中一次的概率为 ,则此射手每次击中的概率是( )
,则此射手每次击中的概率是( )
A. | B.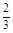 | C. | D. |
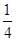
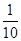

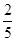

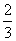



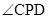 为锐角的概率是
为锐角的概率是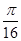
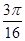
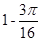
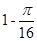

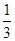
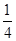
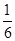
 ,没有平局.采用三局两胜制比赛,即先胜两局者获胜且比赛结束,则甲队获胜的概率等于( )
,没有平局.采用三局两胜制比赛,即先胜两局者获胜且比赛结束,则甲队获胜的概率等于( )