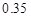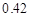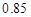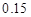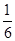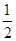题目内容
在一个袋子中装有分别标注1、2、3、4、5的5个形状大小完全相同的小球,现从中随机取出2个小球,则取出小球标注的数字之差的绝对值为2或4的概率是( )
A.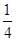 | B.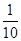 | C. | D.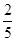 |
D
解析试题分析:这是一个古典概型,只要做出事件总数和满足条件的事件数就可以得到结果,从5个球中任取两个有C52=10种方法,数字之差的绝对值为2或4的有四种结果,根据概率公式得到结果.解:从5个球中任取两个有C52=10种方法,数字之差的绝对值为2或4的有(1,3),(2,4),(3,5),(1,5)四种结果,∴P=4:10=2:5,故选D
考点:古典概型
点评:本题通过列举事件数得到概率,解题时要学会如何判断一个试验是否是古典概型,分清在一个古典概型中某随机事件包含的基本事件的个数和试验中基本事件的总数

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
已知随机变量 服从正态分布
服从正态分布 ,
, ,则
,则 的值等于( )
的值等于( )
| A.0.1 | B.0.2 | C.0.4 | D.0.6 |
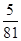
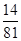
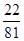
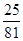
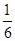 B.
B.  C.
C. 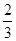 D.
D. 









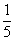
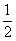
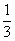
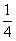
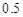 和
和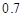 ,则两次射击中至少有一次命中目标的概率是( )
,则两次射击中至少有一次命中目标的概率是( )