题目内容
解答题:解答应写出文字说明,证明过程或演算步骤.
定义F(x,y)=(1+x)y,x,y∈(0,+∞),
(Ⅰ)令函数f(x)=F(1,log2(x2-4x+9))的图象为曲线C1,曲线C1与y轴交于点A(0,m),过坐标原点O向曲线C1作切线,切点为B(n,t)(n>0),设曲线C1在点A、B之间的曲线段与线段OA、OB所围成图形的面积为S,求S的值;
(Ⅱ)令函数g(x)=F(1,log2(x3+ax2+bx+1))的图象为曲线C2,若存在实数b使得曲线C2在x0(-4<x0<-1)处有斜率为-8的切线,求实数a的取值范围;
(Ⅲ)当![]() 且x<y时,证明F(x,y)>F(y,x).
且x<y时,证明F(x,y)>F(y,x).
解析:
|
解:(Ⅰ)∵ ∴ 又过坐标原点O向曲线 ∴ 解得B(3,6), 2分 ∴ (Ⅱ) 设曲线 又由题设log2(x3+ax2+bx+1)>0, ∴存在实数b使得 由(1)得 ∴由 得2×(-4)2+a×(-4)+8>0或2×(-1)2+a×(-1)+8>0, ∴a<10或 ∴ (Ⅲ)令 又令 ∴ ∵ ∴当 ∴当 ∴ ∴ ∴yln(1+x)>xln(1+y), ∴ ∴当 |

| |||||||||||

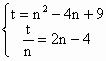 ,
, 有解, 6分
有解, 6分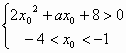 有解,
有解,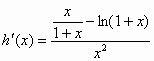 , 10分
, 10分