题目内容
已知二次函数f(x)=ax2+bx+c和“伪二次函数”g(x)=ax2+bx+clnx(abc≠0).(1)证明:只要a<0,无论b取何值,函数g(x)在定义域内不可能总为增函数;
(2)在同一函数图象上任意取不同两点A(x1,y1),B(x2,y2),线段AB中点为C(x,y),记直线AB的斜率为k,
①对于二次函数f(x)=ax2+bx+c,求证:k=f′(x);
②对于“伪二次函数”g(x)=ax2+bx+clnx,是否有①同样的性质?证明你的结论.
【答案】分析:(1)用导函数大于0在定义域内恒成立,结合二次不等式恒成立知不可能,据导数大于0函数单增,得证.
(2)①据两点斜率公式求k,再据中的坐标公式和导数公式得f′(x),得证.
(2)②先假设有得到一个关于t的等式,构造函数,研究函数单调性求最小值,得等式不成立,故假设不成立.
解答:解:(1)如果x>0,g(x)为增函数,则
g′(x)=2ax+b+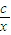 =
= 恒成立.
恒成立.
∴2ax2+bx+c>0(ii)恒成立
∵a<0,由二次函数的性质,(ii)不可能恒成立
则函数g(x)不可能总为增函数.
(2)①对于二次函数:
k=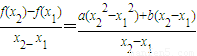 =2ax+b
=2ax+b
由f′(x)=2ax+b故f′(x)=2ax+b
即k=f′(x)
(2)②
不妨设x2>x1,对于伪二次函数g(x)=ax2+bx+clnx=f(x)+clnx-c,
k=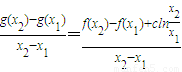
如果有①的性质,则g′(x)=k
∴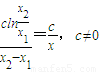
即∴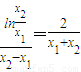 ,
,
令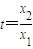 ,t>1,则
,t>1,则
设s(t)=lnt-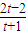 ,则
,则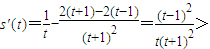
∴s(t)在(1,+∞)上递增,
∴s(t)>s(1)=0
∴g′(x)≠k∴“伪二次函数“g(x)=ax2+bx+clnx不具有①的性质.
点评:本题考查利用导数研究函数的单调性、函数的最值、两点斜率、不等式恒成立问题、构造函数等.
(2)①据两点斜率公式求k,再据中的坐标公式和导数公式得f′(x),得证.
(2)②先假设有得到一个关于t的等式,构造函数,研究函数单调性求最小值,得等式不成立,故假设不成立.
解答:解:(1)如果x>0,g(x)为增函数,则
g′(x)=2ax+b+
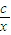 =
= 恒成立.
恒成立.∴2ax2+bx+c>0(ii)恒成立
∵a<0,由二次函数的性质,(ii)不可能恒成立
则函数g(x)不可能总为增函数.
(2)①对于二次函数:
k=
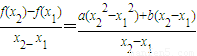 =2ax+b
=2ax+b由f′(x)=2ax+b故f′(x)=2ax+b
即k=f′(x)
(2)②
不妨设x2>x1,对于伪二次函数g(x)=ax2+bx+clnx=f(x)+clnx-c,
k=
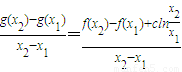
如果有①的性质,则g′(x)=k
∴
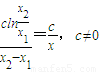
即∴
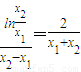 ,
,令
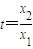 ,t>1,则
,t>1,则
设s(t)=lnt-
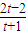 ,则
,则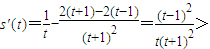
∴s(t)在(1,+∞)上递增,
∴s(t)>s(1)=0
∴g′(x)≠k∴“伪二次函数“g(x)=ax2+bx+clnx不具有①的性质.
点评:本题考查利用导数研究函数的单调性、函数的最值、两点斜率、不等式恒成立问题、构造函数等.

练习册系列答案
 优加精卷系列答案
优加精卷系列答案
相关题目