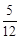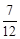题目内容
袋中有12个小球,分别为红球、黑球、黄球、绿球,从中任取一球,已知取到红球的概率是
,取到黑球或黄球的概率是
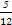,取到黄球或绿球的概率也是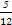,则取到黑球、黄球、绿球的概率分别是 .
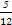,取到黑球或黄球的概率是,取到黄球或绿球的概率也是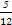,则取到黑球、黄球、绿球的概率分别是 .
,
,设取得红球、黑球、黄球、绿球分别为事件A,B,C, D,则B与C互斥,C与D互斥,设P(B)=x,P(C)=y,P(D)=z,依题意有:
P(A)+P(B)+P(C)+P(D)=+x+y+z=1,
P(B∪C)=P(B)+P(C)=x+y=,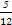
P(C∪D)=P(C)+P(D)=y+z=,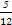
解上式得: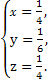
P(A)+P(B)+P(C)+P(D)=
+x+y+z=1,P(B∪C)=P(B)+P(C)=x+y=
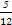,P(C∪D)=P(C)+P(D)=y+z=
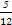,解上式得:
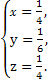
练习册系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
，将这10株树苗的高度依次输入按程序框图进行运算(如图)，问输出的S大小为多少？并说明S的统计学意义；
，
.
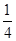
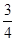
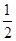
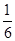
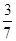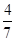)i,i=1,2,3,则a的值是( )
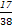
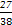
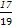
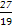
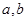，使得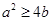
的概率是( )
