题目内容
已知平面向量a=(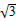 ,-1),b=
,-1),b=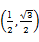 .
.
(1)若x=(t+2)a+(t2-t-5)b,y=-ka+4b(t,k∈R),且x⊥y,求出k关于t的关系式k=f(t).
(2)求函数k=f(t)在t∈(-2,2)上的最小值.
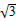 ,-1),b=
,-1),b=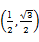 .
.(1)若x=(t+2)a+(t2-t-5)b,y=-ka+4b(t,k∈R),且x⊥y,求出k关于t的关系式k=f(t).
(2)求函数k=f(t)在t∈(-2,2)上的最小值.
(1)k=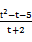 (t≠-2).
(t≠-2).
(2)-3
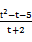 (t≠-2).
(t≠-2).(2)-3
(1)由a=(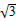 ,-1),b=
,-1),b=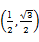 得,a·b=
得,a·b=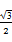 -
-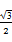 =0.|a|=2,|b|=1.
=0.|a|=2,|b|=1.
因为x⊥y,
所以x·y=[(t+2)a+(t2-t-5)b]·(-ka+4b)=0.
即-k(t+2)a2+4(t2-t-5)b2=0.
4k(t+2)=4(t2-t-5),
k=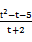 (t≠-2).
(t≠-2).
(2)k=f(t)=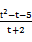 =t+2+
=t+2+ -5.
-5.
因为t∈(-2,2),所以t+2>0.
k≥2 -5=-3.
-5=-3.
当且仅当t+2= ,即t=-1时,“=”成立.
,即t=-1时,“=”成立.
故k的最小值是-3.
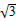 ,-1),b=
,-1),b=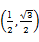 得,a·b=
得,a·b=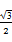 -
-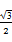 =0.|a|=2,|b|=1.
=0.|a|=2,|b|=1.因为x⊥y,
所以x·y=[(t+2)a+(t2-t-5)b]·(-ka+4b)=0.
即-k(t+2)a2+4(t2-t-5)b2=0.
4k(t+2)=4(t2-t-5),
k=
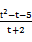 (t≠-2).
(t≠-2).(2)k=f(t)=
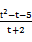 =t+2+
=t+2+ -5.
-5.因为t∈(-2,2),所以t+2>0.
k≥2
 -5=-3.
-5=-3.当且仅当t+2=
 ,即t=-1时,“=”成立.
,即t=-1时,“=”成立.故k的最小值是-3.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目

 的值;
的值;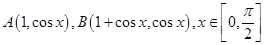 ,
,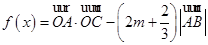 的最小值为
的最小值为 ,求实数m的值.
,求实数m的值.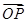 =3a+2b,
=3a+2b,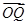 =a+3b,则P,Q两点间的距离为( )
=a+3b,则P,Q两点间的距离为( )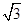

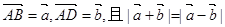 ,则四边形ABCD的形状
,则四边形ABCD的形状 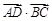 =
=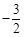 ,则AC=_____ __.
,则AC=_____ __.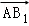 ⊥
⊥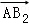 ,|
,|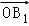 |=|
|=| |=1,
|=1,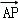 =
=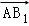 +
+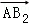 .若|
.若|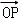 |<
|<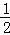 ,则|
,则|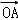 |的取值范围是( )
|的取值范围是( )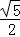 ]
] ]
]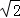 ]
] ,1),B点是以原点O为圆心的单位圆上的动点,则|
,1),B点是以原点O为圆心的单位圆上的动点,则| +
+ |的最大值是( )
|的最大值是( )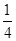 |AB|。若
|AB|。若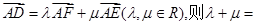 .
. ,且
,且 .当
.当 时,定义平面坐标系
时,定义平面坐标系 为
为 -仿射坐标系,在
-仿射坐标系,在 的斜坐标这样定义:
的斜坐标这样定义: 分别为与
分别为与 轴、
轴、 轴正向相同的单位向量,若
轴正向相同的单位向量,若 ,则记为
,则记为 ,那么在以下的结论中,正确的有.(填上所有正确结论的序号)
,那么在以下的结论中,正确的有.(填上所有正确结论的序号) 、
、 ,若
,若 ,则
,则 ;
; ;
; ,则
,则 ;
; ,则
,则 ;
; 、
、 ,若
,若 与
与 的夹角
的夹角 ,则
,则 .
.