题目内容
12.下列说法中:①函数y=log2(2x-x2)的单调递增区间是(-∞,1);
②若不等式x2+2ax-a≥0对x∈R恒成立,则a的取值范围为[-1,0];
③已知函数f(x)=$\left\{\begin{array}{l}{(3a-2)x+6a-1(x<1)}\\{{a}^{x}(x≥1)}\end{array}\right.$,在(-∞,+∞)上单调递减,那么实数a的取值范围是($\frac{3}{8}$,$\frac{2}{3}$);
④函数f(x)=x2+ax+3(a∈R)在x∈[-1,1]上的最小值是1,则a=3或a=-3.
其中正确说法的序号有②④(注:把你认为是正确的洗好都填上)
分析 根据复合函数的单调性,和对数函数的定义域,求出函数的单调区间,可判断①;根据二次函数的图象和性质,求出a的取值范围,可判断②;根据分段函数的单调性,求出a的取值范围,可判断③;据二次函数的图象和性质,求出a的值,可判断④.
解答 解:①函数y=log2(2x-x2)的定义域为(-∞,0)∪(2,+∞),
当x∈(-∞,0)时,t=2x-x2为增函数,y=log2t为增函数,函数y=log2(2x-x2)为增函数,
故单调递增区间时(-∞,0),故错误;
②若不等式x2+2ax-a≥0对x∈R恒成立,则△=4a2+4a≤0,解得:a∈[-1,0],故正确;
③函数f(x)=$\left\{\begin{array}{l}{(3a-2)x+6a-1(x<1)}\\{{a}^{x}(x≥1)}\end{array}\right.$,在(-∞,+∞)上单调递减,则$\left\{\begin{array}{l}3a-2<0\\ 0<a<1\\ 3a-2+6a-1≥a\end{array}\right.$,解得a∈[$\frac{3}{8}$,$\frac{2}{3}$),故错误;
④函数f(x)=x2+ax+3(a∈R)在x∈[-1,1]上的最小值是1,
若$-\frac{a}{2}$≥1,即a≤-2,则f(1)=4+a=1,解得:a=-3;
若-1<$-\frac{a}{2}$<1,即-2<a<2,则f($-\frac{a}{2}$)=3-$\frac{{a}^{2}}{4}$=1,解得:a=-2$\sqrt{2}$(舍去);
若$-\frac{a}{2}$≤-1,即a≥2,则f(-1)=4-a=1,解得:a=3;
则a=3或a=-3.故正确;
故正确的说法为:②④,
故答案为:②④
点评 本题以命题的真假判断与应用为载体,考查了复合函数,二次函数的图象和性质,分段函数的单调性,难度中档.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案| A. | 已知 a,b,m∈R,命题“若 am2<bm2,则a<b”为真命题 | |
| B. | 命题“$?{x_0}∈R,{x_0}^2-{x_0}>0$”的否定是:“?x∈R,x2-x≤0” | |
| C. | 命题“p且q”为真命题,则命题p和q命题均为真命题 | |
| D. | “x>3”是“x>2”的充分不必要条件 |
| A. | ∅ | B. | (0,+∞) | C. | (-∞,-4)∪(0,+∞) | D. | R |
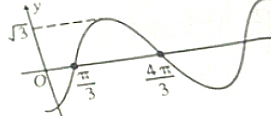 设函数f(x)=Asin(ωx+φ)x∈R,ω>0,|φ|<π),其导函数y=f′(x)的部分图象如图所示,
设函数f(x)=Asin(ωx+φ)x∈R,ω>0,|φ|<π),其导函数y=f′(x)的部分图象如图所示,