题目内容
设直线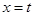 与函数
与函数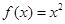 ,
,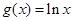 的图象分别交于M、N两点,则当MN达到最小时t的值为
的图象分别交于M、N两点,则当MN达到最小时t的值为

解析试题分析:由题意得: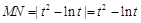 ,设
,设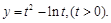 则由
则由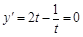 得:
得: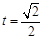 ,当
,当 ,当
,当 ,所以当MN达到最小时t的值为
,所以当MN达到最小时t的值为 .
.
考点:利用导数求最值

练习册系列答案
相关题目
已知函数 的定义域[-1,5],部分对应值如表,
的定义域[-1,5],部分对应值如表, 的导函数
的导函数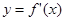 的图象如图所示,下列关于函数
的图象如图所示,下列关于函数 的命题;
的命题;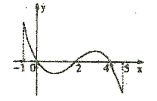
| x | -1 | 0 | 2 | 4 | 5 |
| F(x) | 1 | 2 | 1.5 | 2 | 1 |
①函数
 的值域为[1,2];
的值域为[1,2];②函数
 在[0,2]上是减函数;
在[0,2]上是减函数;③如果当
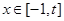 时,
时, 的最大值是2,那么t的最大值为4;
的最大值是2,那么t的最大值为4;④当
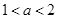 时,函数
时,函数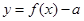 最多有4个零点.
最多有4个零点.其中正确命题的序号是 .
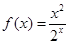 在区间
在区间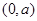 内单调,则
内单调,则 的最大值为__________.
的最大值为__________.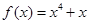 图像上一点,在A处的切线平行于直线
图像上一点,在A处的切线平行于直线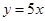 ,则A点坐标为 ;
,则A点坐标为 ;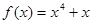 图像上一点,在A处的切线平行于直线
图像上一点,在A处的切线平行于直线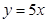 ,则A点坐标为 ;
,则A点坐标为 ;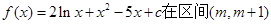 上为递减函数,则m的取值范围是 。
上为递减函数,则m的取值范围是 。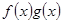 =ax,且f′(x)g(x)+ f(x)·g′(x) <0,
=ax,且f′(x)g(x)+ f(x)·g′(x) <0,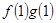 +
+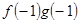 =
=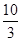 ,若有穷数列{
,若有穷数列{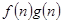 }(n∈N*)的前n项和等于
}(n∈N*)的前n项和等于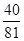 ,则n等于 .
,则n等于 . 左侧的图形的面积为
左侧的图形的面积为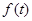 ,则
,则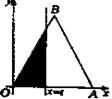
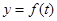 的图像在点P(t0,f(t0))处的切线的斜率为
的图像在点P(t0,f(t0))处的切线的斜率为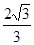 ,则t0=____________.
,则t0=____________. .若曲线
.若曲线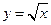 与直线
与直线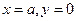 所围成封闭图形的面积为
所围成封闭图形的面积为 ,则
,则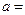 ______.
______.