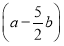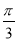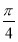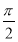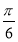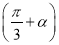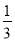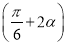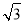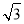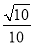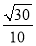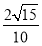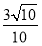题目内容
已知函数f(x)=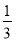 ax3-
ax3-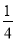 x2+cx+d(a,c,d∈R)满足f(0)=0,f′(1)=0,且f′(x)≥0在R上恒成立.
x2+cx+d(a,c,d∈R)满足f(0)=0,f′(1)=0,且f′(x)≥0在R上恒成立.
(1)求a,c,d的值;
(2)若h(x)=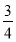 x2-bx+
x2-bx+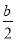 -
-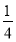 ,解不等式f′(x)+h(x)<0.
,解不等式f′(x)+h(x)<0.
(1)a= ,c=
,c=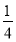 ,d=0(2)当b>
,d=0(2)当b> 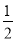 时,解集为
时,解集为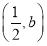 ,当b<
,当b< 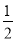 时,解集为
时,解集为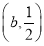 ,当b=
,当b=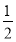 时,解集为
时,解集为
【解析】(1)∵f(0)=0,∴d=0,∵f′(x)=ax2-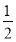 x+c.又f′(1)=0,∴a+c=
x+c.又f′(1)=0,∴a+c=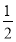 .∵f′(x)≥0在R上恒成立,即ax2-
.∵f′(x)≥0在R上恒成立,即ax2-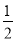 x+c≥0恒成立,∴ax2-
x+c≥0恒成立,∴ax2-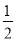 x+
x+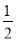 -a≥0恒成立,显然当a=0时,上式不恒成立.∴a≠0,
-a≥0恒成立,显然当a=0时,上式不恒成立.∴a≠0,
∴ 即
即 解得a=
解得a= ,c=
,c=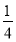 .
.
(2)由(1)知f′(x)=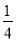 x2-
x2-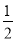 x+
x+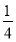 .由f′(x)+h(x)<0,得
.由f′(x)+h(x)<0,得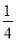 x2-
x2-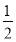 x+
x+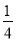 +
+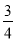 x2-bx+
x2-bx+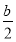 -
-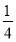 <0,即x2-
<0,即x2-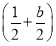 x+
x+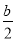 <0,
<0,
即(x-b) 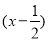 <0,当b>
<0,当b> 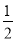 时,解集为
时,解集为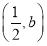 ,
,
当b< 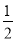 时,解集为
时,解集为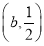 ,当b=
,当b=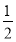 时,解集为
时,解集为 .
.

练习册系列答案
相关题目