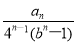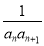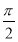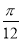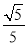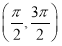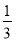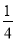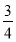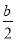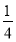题目内容
已知向量a,b满足|a|=2,|b|=1,且(a+b)⊥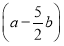 ,则a与b的夹角为( ).
,则a与b的夹角为( ).
A.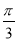 B.
B.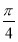 C.
C.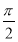 D.
D.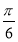
A
【解析】因为(a+b)⊥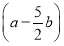 ,所以(a+b)·
,所以(a+b)·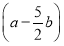 =a2-
=a2-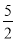 b2-
b2-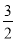 a·b=0.又因为|a|=2,|b|=1,所以4-
a·b=0.又因为|a|=2,|b|=1,所以4-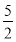 -
-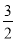 a·b=0.所以a·b=1.又a·b=|a||b|cos〈a,b〉=1,所以cos〈a,b〉=
a·b=0.所以a·b=1.又a·b=|a||b|cos〈a,b〉=1,所以cos〈a,b〉=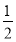 .又a与b的夹角的取值范围是[0,π],所以a与b的夹角为
.又a与b的夹角的取值范围是[0,π],所以a与b的夹角为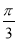 .
.

练习册系列答案
相关题目