题目内容
已知函数f(x)在(0,+∞)上满足f(xy)=f(x)+f(y),且f(x)在定义域内是减函数.(1)求f(1)的值;
(2)若f(2a-3)<0,试确定a的取值范围.
【答案】分析:(1)由函数f(x)在(0,+∞)上满足f(xy)=f(x)+f(y),令x=y=1,能求出f(1)=0.
(2)由f(x)在定义域内是减函数,f(2a-3)<0=f(1),知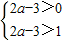 ,由此能求出a的取值范围.
,由此能求出a的取值范围.
解答:解:(1)∵函数f(x)在(0,+∞)上满足f(xy)=f(x)+f(y),
∴f(1)=f(1)+f(1),解得f(1)=0.
(2)∵f(x)在定义域内是减函数,f(2a-3)<0=f(1),
∴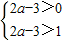 ,解得a>2.
,解得a>2.
∴a的取值范围是(2,+∞).
点评:本题考查抽象函数的性质及其应用,解题时要认真审题,注意等价转化思想的合理运用.
(2)由f(x)在定义域内是减函数,f(2a-3)<0=f(1),知
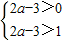 ,由此能求出a的取值范围.
,由此能求出a的取值范围.解答:解:(1)∵函数f(x)在(0,+∞)上满足f(xy)=f(x)+f(y),
∴f(1)=f(1)+f(1),解得f(1)=0.
(2)∵f(x)在定义域内是减函数,f(2a-3)<0=f(1),
∴
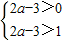 ,解得a>2.
,解得a>2.∴a的取值范围是(2,+∞).
点评:本题考查抽象函数的性质及其应用,解题时要认真审题,注意等价转化思想的合理运用.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
已知函数f(x)在R上满足y=f(x)=2f(2-x)+ex-1+x2,则曲线y=f(x)在点(1,f(1))处的切线方程是( )
| A、2x-y-1=0 | B、x-y-3=0 | C、3x-y-2=0 | D、2x+y-3=0 |