题目内容
已知函数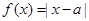 .
.
(1)若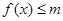 的解集为
的解集为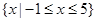 ,求实数
,求实数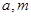 的值.
的值.
(2)当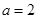 且
且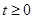 时,解关于
时,解关于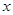 的不等式
的不等式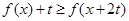 .
.
【答案】
(1)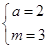 ;(2)当
;(2)当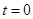 时,原不等式的解集为
时,原不等式的解集为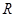 ,当
,当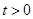 时,原不等式的解集为
时,原不等式的解集为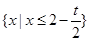 .
.
【解析】
试题分析:本题考查绝对值不等式的解法及利用解集求实数的值,考查学生的分类讨论思想和转化能力.第一问,利用绝对值不等式的解法求出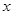 的范围,让它和已知解集相同,列出等式,解出
的范围,让它和已知解集相同,列出等式,解出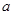 和
和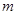 的值;第二问,先将
的值;第二问,先将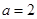 代入,得到
代入,得到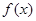 解析式,再代入到所求不等式中,找到需要解的不等式,注意到当
解析式,再代入到所求不等式中,找到需要解的不等式,注意到当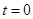 时,2个绝对值一样,所以先进行讨论,当
时,2个绝对值一样,所以先进行讨论,当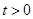 时,按照解绝对值不等式的步骤,先列出不等式组,内部求交集,综合
时,按照解绝对值不等式的步骤,先列出不等式组,内部求交集,综合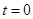 和
和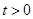 的情况得到结论.
的情况得到结论.
试题解析:(Ⅰ)由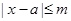 得
得 ,
,
所以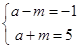 解之得
解之得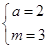 为所求.
4分
为所求.
4分
(Ⅱ)当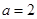 时,
时, ,
,
所以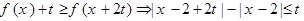
当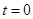 时,不等式①恒成立,即
时,不等式①恒成立,即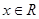 ;
;
当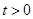 时,不等式
时,不等式
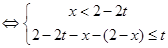 或
或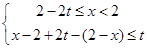 或
或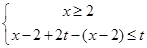 ,
,
解得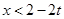 或
或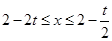 或
或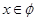 ,即
,即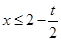 ;
;
综上,当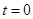 时,原不等式的解集为
时,原不等式的解集为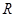 ,
,
当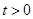 时,原不等式的解集为
时,原不等式的解集为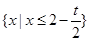 . 10分
. 10分
考点:1.绝对值不等式的解法.

练习册系列答案
相关题目
 ,
,
 ,求
,求 的单调区间;
的单调区间; 时,求证:
时,求证: .
.
 .
. 为
为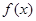 的极值点,求实数
的极值点,求实数 的值;
的值; 在
在 上为增函数,求实数
上为增函数,求实数 时,方程
时,方程 有实根,求实数
有实根,求实数 的最大值.
的最大值. 。
。 ,求函数
,求函数 的值;
的值; .
.
 中任取一个元素
中任取一个元素 ,从集合
,从集合 中任取一个元素
中任取一个元素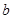 ,求方程
,求方程 有两个不相等实根的概率;
有两个不相等实根的概率; 中任取的一个数,
中任取的一个数, 中任取的一个数,求方程
中任取的一个数,求方程