题目内容
设三棱柱ABC-A1B1C1的体积为V,P、Q分别是侧棱AA1、CC1上的点,且PA=QC1,则四棱锥B-APQC的体积为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
分析:由已知中三棱柱ABC-A1B1C1的体积为V,P、Q分别是侧棱AA1、CC1上的点,且PA=QC1,我们可得SAPQC=
SACC1A1,即VB-APQC=
VB-ACC1A1,再结合同底等高的棱柱的体积为棱锥体积的3倍,即可求出答案.
| 1 |
| 2 |
| 1 |
| 2 |
解答:解:∵三棱柱ABC-A1B1C1的体积为V,
又∵P、Q分别是侧棱AA1、CC1上的点,且PA=QC1,
∴四棱锥B-APQC的底面积SAPQC=
SACC1A1
又VB-ACC1A1=V三棱柱ABC-A1B1C1-V三棱锥B-A1B1C1=V-
V=
V
∴VB-APQC=
VB-ACC1A1=
•
V=
V
故选C.
又∵P、Q分别是侧棱AA1、CC1上的点,且PA=QC1,
∴四棱锥B-APQC的底面积SAPQC=
| 1 |
| 2 |
又VB-ACC1A1=V三棱柱ABC-A1B1C1-V三棱锥B-A1B1C1=V-
| 1 |
| 3 |
| 2 |
| 3 |
∴VB-APQC=
| 1 |
| 2 |
| 1 |
| 2 |
| 2 |
| 3 |
| 1 |
| 3 |
故选C.
点评:本题考查的知识点是棱柱的体积、棱锥的体积,其中分析出棱锥与原棱柱之间底面积、高之间的比例关系是解答本题的关键.

练习册系列答案
相关题目
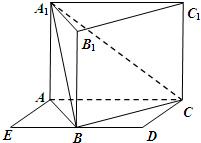 如图,侧棱垂直底面的三棱柱ABC-A1B1C1的底面ABC位于平行四边形ACDE中,AE=2,AC=AA1=4,∠E=60°,点B为DE中点.
如图,侧棱垂直底面的三棱柱ABC-A1B1C1的底面ABC位于平行四边形ACDE中,AE=2,AC=AA1=4,∠E=60°,点B为DE中点.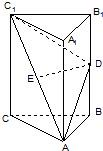 如图,在直三棱柱ABC-A1B1C1中,AB=BC,D、E分别为BB1、AC1的中点.
如图,在直三棱柱ABC-A1B1C1中,AB=BC,D、E分别为BB1、AC1的中点. 在三棱柱ABC-A1B1C1中,AB=AC=AA1=2,平面ABC1⊥平面AA1C1C,∠AA1C1=∠BAC1=60°,设AC1与AC相交于点O,如图.
在三棱柱ABC-A1B1C1中,AB=AC=AA1=2,平面ABC1⊥平面AA1C1C,∠AA1C1=∠BAC1=60°,设AC1与AC相交于点O,如图. 如图在 正三棱柱ABC-A1 B1 C1中,底面边长为
如图在 正三棱柱ABC-A1 B1 C1中,底面边长为 (2013•四川)如图,在三棱柱ABC-A1B1C中,侧棱AA1⊥底面ABC,AB=AC=2AA1=2,∠BAC=120°,D,D1分别是线段BC,B1C1的中点,P是线段AD上异于端点的点.
(2013•四川)如图,在三棱柱ABC-A1B1C中,侧棱AA1⊥底面ABC,AB=AC=2AA1=2,∠BAC=120°,D,D1分别是线段BC,B1C1的中点,P是线段AD上异于端点的点.