题目内容
设幂函数f（x）=（a-1）xk（a∈R，k∈Q）的图象过点（
，2）．
（1）求a，k的值；
（2）若函数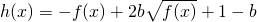
在[0，1]上的最大值为2，求实数b的值．
解：（1）∵幂函数f（x）=（a-1）xk（a∈R，k∈Q）的图象过点（，2），
∴a-1=1，a=2．
，∴k=2．
（2）由（1）知f（x）=x2，
∵，
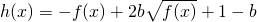∴h（x）=-x2+2bx+1-b=-（x-b）2+b2-b+1，x∈[0，1]，
当b≥1时，hmax=h（1）=b=2，
当0＜b＜1时，hmax=h（b）=b2-b+1=2，
∴b=
（舍）．
当b≤0时，
hmax=h（0）=1-b=2，
∴b=-1．
综上：b=2或b=-1．
分析：（1）由幂函数的定义知a-1=1，由f（x）=（a-1）xk（a∈R，k∈Q）的图象过点（，2），知，由此能求出a，k．
（2）由（1）知f（x）=x2，由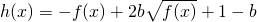，知h（x）=-x2+2bx+1-b=-（x-b）2+b2-b+1，x∈[0，1]，再由分类讨论思想能求出实数b的值．
点评：本题考查幂函数的性质和应用，是基础题．解题时要认真审题，仔细解答，注意配方法和分类讨论思想的灵活运用．
，2），∴a-1=1，a=2．
，∴k=2．（2）由（1）知f（x）=x2，
∵
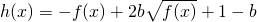，∴h（x）=-x2+2bx+1-b=-（x-b）2+b2-b+1，x∈[0，1]，
当b≥1时，hmax=h（1）=b=2，
当0＜b＜1时，hmax=h（b）=b2-b+1=2，
∴b=
（舍）．当b≤0时，
hmax=h（0）=1-b=2，
∴b=-1．
综上：b=2或b=-1．
分析：（1）由幂函数的定义知a-1=1，由f（x）=（a-1）xk（a∈R，k∈Q）的图象过点（
，2），知，由此能求出a，k．（2）由（1）知f（x）=x2，由
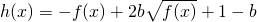，知h（x）=-x2+2bx+1-b=-（x-b）2+b2-b+1，x∈[0，1]，再由分类讨论思想能求出实数b的值．点评：本题考查幂函数的性质和应用，是基础题．解题时要认真审题，仔细解答，注意配方法和分类讨论思想的灵活运用．
练习册系列答案
相关题目