题目内容
已知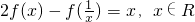 且x≠0.
且x≠0.
(Ⅰ)求函数f(x)的解析式;
(Ⅱ)求函数f(x)的值域.
解:(1)在 中,…①…
中,…①…
以 代替x,得
代替x,得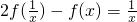 ,…②…
,…②…
①×2+②,得 ,
,
所以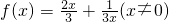 .
.
所以函数f(x)的解析式为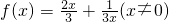 .
.
(2)由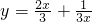 得3xy=2x2+1,即2x2-3y•x+1=0.
得3xy=2x2+1,即2x2-3y•x+1=0.
因为x≠0,x∈R,所以关于x的方程2x2-3y•x+1=0有实数根.故△=9y2-8≥0,即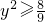 .
.
解得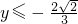 ,或
,或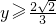 .
.
所以函数f(x)的值域为 .
.
分析:(1)利用方程组法求解该函数的解析式;(2)将函数最值问题转化为方程有根问题求解.
点评:本题考察构造方程利用方程组法求函数解析式、函数最值的求解,(2)中函数单调性比较难判断,所以采用转化思想解答.
 中,…①…
中,…①…以
 代替x,得
代替x,得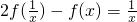 ,…②…
,…②…①×2+②,得
 ,
,所以
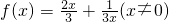 .
.所以函数f(x)的解析式为
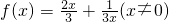 .
.(2)由
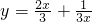 得3xy=2x2+1,即2x2-3y•x+1=0.
得3xy=2x2+1,即2x2-3y•x+1=0.因为x≠0,x∈R,所以关于x的方程2x2-3y•x+1=0有实数根.故△=9y2-8≥0,即
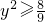 .
.解得
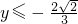 ,或
,或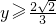 .
.所以函数f(x)的值域为
 .
.分析:(1)利用方程组法求解该函数的解析式;(2)将函数最值问题转化为方程有根问题求解.
点评:本题考察构造方程利用方程组法求函数解析式、函数最值的求解,(2)中函数单调性比较难判断,所以采用转化思想解答.

练习册系列答案
相关题目
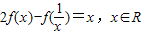 且x≠0.
且x≠0.