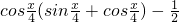Question

设函数y=f（x）满足对一切的x∈R，f（x）≥0，且f(x+1)=

9-f2(x)

，已知当x∈[0，1）时，f(x)=

2x，0≤x≤ 1 2 lg(x+31) 1 2 ＜x＜1

，则f(

100

)=

 

．

Answer 1

分析：利用函数周期性解题，关键是求出周期．

解答：_解：∵f（x+3）═f[（x+2）+1]=

9-f2(x+2)

=

9-9+f2(x+1)

=f(x+1)
∴T=2
∴f（

100

）=f（10）=f（0）=2⁰=1，
故答案为：1．

点评：本题主要考查利用函数周期性化简求值．也可以直接求出f（0）、f（1）、、、f（10）或利用规律得出f（10）=1