题目内容
二次函数y=a(a+1)x2-(2a+1)x+1,当a=1,2,3,…,n,…时,其图象在x轴上截得的弦长依次为d1,d2,…,dn,…,则A.4 B.3 C.2 D.1
答案:D
【解析】设二次函数y=a(a+1)x2-(2a+1)x+1与x轴的分布交点为(x1,0),(x2,0),则令y=0得a(a+1)x2-(2a+1)x+1=0,∴(ax-1)[(a+1)x-1)=0,解之得x1=![]() ,x2=
,x2=![]() .∴弦长da=|x1-x2|=
.∴弦长da=|x1-x2|=![]() ,令a=1,2,3,…,n得d1+d2+…+dn
,令a=1,2,3,…,n得d1+d2+…+dn
=(1-![]() )+(
)+(![]() )+…+
)+…+![]()
∴![]() (d1+d2+…+dn)=
(d1+d2+…+dn)= ![]() (1-
(1-![]() )=1.
)=1.

练习册系列答案
相关题目
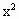 -(2a+1)x+1,当a=1,2,3,…,n时,其抛物线在x轴上截得的线段的长度依次是
-(2a+1)x+1,当a=1,2,3,…,n时,其抛物线在x轴上截得的线段的长度依次是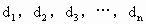 ,则
,则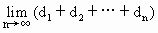 的值是________.
的值是________.