题目内容
一个球面上有三个点A、B、C，若AB=AC=2，BC=2
，球心到平面ABC的距离为1，则球的表面积为（ ）
| 2 |
| A．3π | B．4π | C．8π | D．12π |
∵△ABC中，AB=AC=2，BC=2
，
∴AB2+AC2=8=BC2，得△ABC是以BC为斜边的等腰直角三角形．
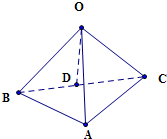
因此BC的中点D为△ABC的外接圆的圆心，
设球心为点O，连结OD，可得OD⊥平面ABC，
∵球心到平面ABC的距离OD=1，BD=
BC=
，
∴Rt△BOD中，OB=
=
，即球的半径R=
．
由此可得球的表面积S=4πR2=12π．
故选：D
| 2 |
∴AB2+AC2=8=BC2，得△ABC是以BC为斜边的等腰直角三角形．
因此BC的中点D为△ABC的外接圆的圆心，
设球心为点O，连结OD，可得OD⊥平面ABC，
∵球心到平面ABC的距离OD=1，BD=
| 1 |
| 2 |
| 2 |
∴Rt△BOD中，OB=
| OD2+BD2 |
| 3 |
| 3 |
由此可得球的表面积S=4πR2=12π．
故选：D
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
