题目内容
由13=12,13+23=(1+2)2,13+23+33=(1+2+3)2,
13+23+33+43=(1+2+3+4)2,……试猜想13+23+33+…+n3= ( )
)
13+23+33+43=(1+2+3+4)2,……试猜想13+23+33+…+n3= (
 )
)
解:由13=12,13+23=(1+2)2,13+23+33=(1+2+3)2,
13+23+33+43=(1+2+3+4)2,,可知等式左边表示的为,连续自然数的立方和,右边是和的完全平方,根据已知中的特点可以猜想,n个自然数的立方和13+23+33+…+n3= (
( )
)
13+23+33+43=(1+2+3+4)2,,可知等式左边表示的为,连续自然数的立方和,右边是和的完全平方,根据已知中的特点可以猜想,n个自然数的立方和13+23+33+…+n3=
 (
( )
)
练习册系列答案
相关题目
 满足
满足 ,
, ,
, 且点P1的坐标是(1,-1)。
且点P1的坐标是(1,-1)。 的方程;
的方程; 与(1)中直线
与(1)中直线
 个图有
个图有 条线段,则
条线段,则 .
. 满足:
满足: ,若前2010项中,恰好含有666项为0,则
,若前2010项中,恰好含有666项为0,则 的值为
的值为  :
: ,
, 时具有性质
时具有性质 对任意的
对任意的 ,
, 与
与 两数中至少有一个是该数列中的一项,现给出以下四个命题:
两数中至少有一个是该数列中的一项,现给出以下四个命题: 具有性质
具有性质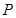 ;
; 具有性质
具有性质 ;
; 具有性质
具有性质 。
。 中,已知
中,已知 且
且 ,则
,则 _______
_______ ;
; ,则G必是
,则G必是 a与b的等比中项;
a与b的等比中项; 是常数数列 a,a,a,·····,则
是常数数列 a,a,a,·····,则 (a,b,c为实常数),则必有:c=0.
(a,b,c为实常数),则必有:c=0. 中,
中, ,
,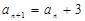 ,若
,若 ,则
,则 =( )
=( ) ),则an= ( )
),则an= ( )