Question

【题目】如图，已知直三棱柱ABC﹣A1B1C1的侧面ACC1A1是正方形，AC=BC，点O是侧面ACC1A1的中心，∠ACB= ，M在棱BC上，且MC=2BM=2．

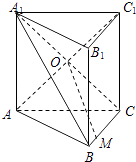
（1）证明BC⊥AC1；
（2）求OM的长度．

Answer 1

【答案】
（1）证明：因为ABC﹣A1B1C1是直三棱柱，

所以CC1⊥底面ABC，

所以CC1⊥BC，

又∠ACB= ，即BC⊥AC，

而CC1，AC面ACC1A1，且CC1∩AC=C，

所以BC⊥面ACC1A1，

而AC1面ACC1A1，

所以BC⊥AC1

（2）解：由（1）可知BC⊥OC，

因为MC=2，OC= ，

所以OM= =

【解析】（1）推导出CC1⊥BC，BC⊥AC，从而BC⊥面ACC1A1 ， 进而BC⊥AC1；（2）由（1）可知BC⊥OC，利用勾股定理求OM的长度．
【考点精析】认真审题，首先需要了解棱柱的结构特征(两底面是对应边平行的全等多边形；侧面、对角面都是平行四边形；侧棱平行且相等；平行于底面的截面是与底面全等的多边形)．