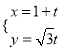题目内容
【题目】选修4-4:坐标系与参数方程
在直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数,
为参数, ![]() ).以原点
).以原点![]() 为极点,以
为极点,以![]() 轴正半轴为极轴,与直角坐标系
轴正半轴为极轴,与直角坐标系![]() 取相同的长度单位,建立极坐标系.设曲线
取相同的长度单位,建立极坐标系.设曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(Ⅰ)设![]() 为曲线
为曲线![]() 上任意一点,求
上任意一点,求![]() 的取值范围;
的取值范围;
(Ⅱ)若直线![]() 与曲线
与曲线![]() 交于两点
交于两点![]() ,
, ![]() ,求
,求![]() 的最小值.
的最小值.
【答案】(1)![]() (2)4.
(2)4.
【解析】试题分析: (1)将曲线C的极坐标方程化为直角坐标方程,将![]() 化为关于
化为关于![]() 的二次函数,求出范围; (2)将直线
的二次函数,求出范围; (2)将直线![]() 的参数方程代入曲线C的直角坐标方程中,由直线参数方程的几何意义求出
的参数方程代入曲线C的直角坐标方程中,由直线参数方程的几何意义求出![]() 表达式,求出最小值.
表达式,求出最小值.
试题解析:(1)将曲线![]() 的极坐标方程
的极坐标方程![]() 化为直角坐标方程为
化为直角坐标方程为![]() ,
,
∵![]() 为曲线
为曲线![]() 上任意一点,∴
上任意一点,∴![]() ,
,
∴![]() 的取值范围是
的取值范围是![]() ;
;
(2)将![]() 代入
代入![]() ,整理,得
,整理,得![]() ,
,
∴![]() ,设方程
,设方程![]() 的两根分别为
的两根分别为![]() ,
,
所以![]() ,
,
当![]() 时,
时, ![]() 取得最小值4.
取得最小值4.

练习册系列答案
相关题目
【题目】为了调查喜欢旅游是否与性别有关,调查人员就“是否喜欢旅游”这个问题,在火车站分别随机调研了![]() 名女性或
名女性或![]() 名男性,根据调研结果得到如图所示的等高条形图.
名男性,根据调研结果得到如图所示的等高条形图.
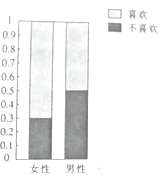
(1)完成下列 ![]() 列联表:
列联表:
喜欢旅游 | 不喜欢旅游 | 估计 | |
女性 | |||
男性 | |||
合计 |
(2)能否在犯错误概率不超过![]() 的前提下认为“喜欢旅游与性别有关”.
的前提下认为“喜欢旅游与性别有关”.
附:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
参考公式:
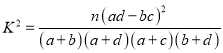 ,其中
,其中![]()
【题目】某高中在校学生2 000人,高一年级与高二年级人数相同并且都比高三年级多1人.为了响应市教育局“阳光体育”号召,该校开展了跑步和跳绳两项比赛,要求每人都参加而且只参加其中一项,各年级参与项目人数情况如下表:
年级 项目 | 高一年级 | 高二年级 | 高三年级 |
跑步 | a | b | c |
跳绳 | x | y | z |
其中a∶b∶c=2∶3∶5,全校参与跳绳的人数占总人数的![]() . 为了了解学生对本次活动的满意度,采用分层抽样从中抽取一个200人的样本进行调查,则高二年级中参与跑步的同学应抽取多少人?
. 为了了解学生对本次活动的满意度,采用分层抽样从中抽取一个200人的样本进行调查,则高二年级中参与跑步的同学应抽取多少人?