题目内容
设抛物线C1:y2=4mx(m>0)的准线与x轴交于点F1,焦点为F2;椭圆C2以F1、F2为焦点,离心率e=
.
(I)(文科做)当m=1时,
①求椭圆C2的标准方程;
②若直线l与抛物线交于A、B两点,且线段AB恰好被点P(3,2)平分,设直线l与椭圆C2交于M、N两点,求线段MN的长;
(II)(仅理科做)设抛物线C1与椭圆C2的一个交点为Q,是否存在实数m,,使得△QF1F2的边长是连续的自然数?若存在,求出这样的实数m的值;若不存在,请说明理由.
| 1 | 2 |
(I)(文科做)当m=1时,
①求椭圆C2的标准方程;
②若直线l与抛物线交于A、B两点,且线段AB恰好被点P(3,2)平分,设直线l与椭圆C2交于M、N两点,求线段MN的长;
(II)(仅理科做)设抛物线C1与椭圆C2的一个交点为Q,是否存在实数m,,使得△QF1F2的边长是连续的自然数?若存在,求出这样的实数m的值;若不存在,请说明理由.
分析:(I)①当m=1时,抛物线C1方程可知,所以椭圆C2中c与a值可求,进而得出椭圆的标准方程;
②由题意得,若x=3,则y=±2
,线段AB不可能被点P(3,2)平分.直线l的斜率k一定存在,不妨设直线l的方程为:y-2=k(x-3),A(x1,y1),B(x2,y2),将直线的方程代入椭圆的方程,消去x得到关于y的一元二次方程,再结合根系数的关系利用中点坐标公式即可求得k值,从而求得直线l的方程.
(II)先假设存在实数m,使得△QF1F2的边长是连续的自然数,由P点为抛物线与椭圆在第一象限的焦点,所以只要根据抛物线方程求出椭圆方程,再联立,即可得出Q点坐标,从而分别求出△QF1F2的三边长,让三边成公差为1得等差数列,求m的值,若能求出,则存在,若不能求出,则不存在.
②由题意得,若x=3,则y=±2
| 3 |
(II)先假设存在实数m,使得△QF1F2的边长是连续的自然数,由P点为抛物线与椭圆在第一象限的焦点,所以只要根据抛物线方程求出椭圆方程,再联立,即可得出Q点坐标,从而分别求出△QF1F2的三边长,让三边成公差为1得等差数列,求m的值,若能求出,则存在,若不能求出,则不存在.
解答:解:(I)①∵c1:y2=4mx的右焦点F2(m,0)∴椭圆的半焦距c=m,
又e=
,∴椭圆的长半轴的长a=2m,短半轴的长b=
m.
椭圆方程为
+
=1,
∴当m=1时,故椭圆方程为
+
=1.
②由题意得,若x=3,则y=±2
,线段AB不可能被点P(3,2)平分,
∴直线l的斜率k一定存在,不妨设直线l的方程为:y-2=k(x-3),A(x1,y1),B(x2,y2)
由
得ky2-4y-12k+8=0,
∴y1+y2=
=4,∴k=1,
∴直线l的方程为:y-2=x-3,即y=x-1.
(II)假设存在满足条件的实数m,
由
,解得:Q(
m,
m),
∴|QF2|=
m+m=
m,|QF1|=4m-|QF2|=
m,又|F1F2|=2m=
m.
即△QF1F2的边长分别是
m、
m、
m.
∵
-
=
-
=1∴m=3,
故存在实数m使△PF1F2的边长是连续的自然数.
又e=
| 1 |
| 2 |
| 3 |
椭圆方程为
| x2 |
| 4m2 |
| y2 |
| 3m2 |
∴当m=1时,故椭圆方程为
| x2 |
| 4 |
| y2 |
| 3 |
②由题意得,若x=3,则y=±2
| 3 |
∴直线l的斜率k一定存在,不妨设直线l的方程为:y-2=k(x-3),A(x1,y1),B(x2,y2)
由
|
∴y1+y2=
| 4 |
| k |
∴直线l的方程为:y-2=x-3,即y=x-1.
(II)假设存在满足条件的实数m,
由
|
| 2 |
| 3 |
| 8 |
| 3 |
∴|QF2|=
| 2 |
| 3 |
| 5 |
| 3 |
| 7 |
| 3 |
| 6 |
| 3 |
即△QF1F2的边长分别是
| 5 |
| 3 |
| 6 |
| 3 |
| 7 |
| 3 |
∵
| 6m |
| 3 |
| 5m |
| 3 |
| 7m |
| 3 |
| 6m |
| 3 |
故存在实数m使△PF1F2的边长是连续的自然数.
点评:本题考查抛物线和椭圆的标准方程和简单性质,弦长公式的应用,考查了椭圆、抛物线与直线的位置关系以及存在性问题,综合性强,做题时认真观察,找出切入点.

练习册系列答案
相关题目
 如图,设抛物线C1:y2=4mx(m>0)的准线与x轴交于F1,焦点为F2;以F1,F2为焦点,离心率e=
如图,设抛物线C1:y2=4mx(m>0)的准线与x轴交于F1,焦点为F2;以F1,F2为焦点,离心率e= 如图,设抛物线C1:y2=4mx(m>0)的准线与x轴交于F1,焦点为F2;以F1,F2为焦点,离心率e=
如图,设抛物线C1:y2=4mx(m>0)的准线与x轴交于F1,焦点为F2;以F1,F2为焦点,离心率e=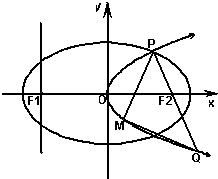 如图,设抛物线C1:y2=4mx(m>0)的准线与x轴交于点F1,焦点为F2;以F1,F2为焦点,离心率为
如图,设抛物线C1:y2=4mx(m>0)的准线与x轴交于点F1,焦点为F2;以F1,F2为焦点,离心率为 如图所示,设抛物线C1:y2=4mx(m>0)的焦点为F2,且其准线与x轴交于F1,以F1,F2为焦点,离心率e=
如图所示,设抛物线C1:y2=4mx(m>0)的焦点为F2,且其准线与x轴交于F1,以F1,F2为焦点,离心率e=