题目内容
已知二次函数 满足以下两个条件:
满足以下两个条件:
①不等式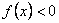 的解集是(-2,0) ②函数
的解集是(-2,0) ②函数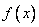 在
在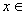
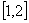 上的最小值是3
上的最小值是3
(Ⅰ)求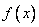 的解析式;
的解析式;
(Ⅱ)若点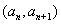
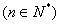 在函数
在函数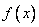 的图象上,且
的图象上,且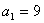
(ⅰ)求证:数列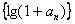 为等比数列
为等比数列
(ⅱ)令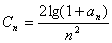 ,是否存在整数
,是否存在整数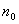 使得数列
使得数列 取到最小值?若有,请求出
取到最小值?若有,请求出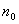 的值;没有,请说明理由。
的值;没有,请说明理由。
【答案】
解:(Ⅰ)∵ f(x)< 0 的解集为(-2,0),且f(x)是二次函数
∴ 可设 f(x)= a x(x + 2) (a > 0),故 f(x)的对称轴为直线 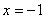 ,
,
∴ f(x)在 [1,2]上的最小值为f(1)=3a =3 ,
∴ a = 1 ,所以f(x)= x 2 + 2 x .
(Ⅱ)(ⅰ)∵ 点(a n , a n + 1 )在函数f(x)= x 2 + 2 x 的图象上
∴ a n + 1 = a n 2 + 2 a n , 则 1 + a n + 1 = 1 + a n 2 + 2 a n = (1 + a n)2
∴ 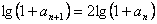 , 又首项
, 又首项 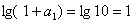
∴ 数列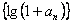 为等比数列,且公比为2 。
为等比数列,且公比为2 。
(ⅱ)由上题可知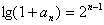 ,
,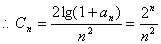 ,
,
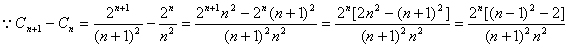
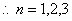 时,有
时,有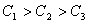 ,
,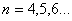 时,有
时,有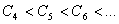
故只须比较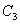 与
与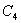 ,而
,而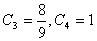 ,所以当
,所以当 时,数列
时,数列 取到最小值。
取到最小值。

练习册系列答案
 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
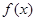 满足以下两个条件:
满足以下两个条件: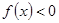 的解集是(-2,0) ②函数
的解集是(-2,0) ②函数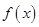 在
在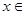
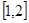 上的最小值是3
上的最小值是3 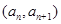
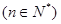 在函数
在函数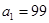
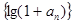 为等比数列
为等比数列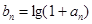 ,是否存在正实数
,是否存在正实数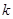 ,使不等式
,使不等式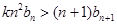 对于一切的
对于一切的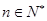 恒成立?若存在,指出
恒成立?若存在,指出