题目内容
某工厂生产甲、乙两种产品,每种产品都是经过第一和第二工序加工而成,两道工序的加工结果相互独立,每道工序的加工结果均有A、B两个等级.对每种产品,两道工序的加工结果都为A级时,产品为一等品,其余均为二等品.(Ⅰ)已知甲、乙两种产品每一道工序的加工结果为A级的概率如表一所示,分别求生产出的甲、乙产品为一等品的概率P甲、P乙;
| 产品\概率\工序 | 第一工序 | 第二工序 |
| 甲 | 0.8 | 0.85 |
| 乙 | 0.75 | 0.8 |
| 产品\利润\等级 | 一等 | 二等 |
| 甲 | 5(万元) | 2.5(万元) |
| 乙 | 2.5(万元) | 1.5(万元) |
| 产品\用量\项目 | 工人(名) | 资金(万元) |
| 甲 | 8 | 5 |
| 乙 | 2 | 10 |
分析:这是一道概率,分布列、数学期望与线性规划的综合问题,(1)根据两道工序的加工结果都为A级时,产品为一等品,故生产出的甲、乙产品为一等品的概率P甲、P乙就是求甲乙两种产品的两道工序的加工结果都为A级的概率.(2)我们要根据题目已知,分别求出随机变量ξ、η的取值,并分析每总取值的概率,即可得到随机变量ξ、η的分布列,进而求出各自的数学期望.(3)由(2)的结论,我们不难得到x,y满足的不等关系,即约束条件,和目标函数,用线性规划的方法解决问题.
解答: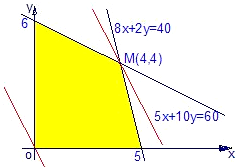 解:(Ⅰ)P甲=0.8×0.85=0.68,P乙=0.75×0.8=0.6.
解:(Ⅰ)P甲=0.8×0.85=0.68,P乙=0.75×0.8=0.6.
(Ⅱ)随机变量ξ、η的分别列是
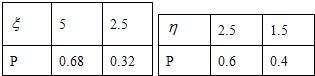
Eξ=5×0.68+2.5×0.32=4.2,Eη=2.5×0.6+1.5×0.4=2.1.
(Ⅲ)由题设知
目标函数为z=xEξ+yEη=4.2x+2.1y.
作出可行域(如图):
作直线l:4.2x+2.1y=0,
将l向右上方平移至l1位置时,直线经过可行域上的点M点与原点距离最大,
此时z=4.2x+2.1y
取最大值.解方程组
得x=4,y=4.即x=4,y=4时,z取最大值,z的最大值为25.2.
 解:(Ⅰ)P甲=0.8×0.85=0.68,P乙=0.75×0.8=0.6.
解:(Ⅰ)P甲=0.8×0.85=0.68,P乙=0.75×0.8=0.6.(Ⅱ)随机变量ξ、η的分别列是

Eξ=5×0.68+2.5×0.32=4.2,Eη=2.5×0.6+1.5×0.4=2.1.
(Ⅲ)由题设知
|
目标函数为z=xEξ+yEη=4.2x+2.1y.
作出可行域(如图):
作直线l:4.2x+2.1y=0,
将l向右上方平移至l1位置时,直线经过可行域上的点M点与原点距离最大,
此时z=4.2x+2.1y
取最大值.解方程组
|
得x=4,y=4.即x=4,y=4时,z取最大值,z的最大值为25.2.
点评:用图解法解决线性规划问题时,分析题目的已知条件,找出约束条件和目标函数是关键,可先将题目中的量分类、列出表格,理清头绪,然后列出不等式组(方程组)寻求约束条件,并就题目所述找出目标函数.然后将可行域各角点的值一一代入,最后比较,即可得到目标函数的最优解.

练习册系列答案
 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案
相关题目
 18、某工厂生产甲、乙两种产品,每种产品都是经过第一道和第二道工序加工而成,两道工序的加工结果相互独立,每道工序的加工结果均有A、B两个等级,对每种产品,两道工序的加工结果都为A级时,产品为一等品,其余均为二等品
18、某工厂生产甲、乙两种产品,每种产品都是经过第一道和第二道工序加工而成,两道工序的加工结果相互独立,每道工序的加工结果均有A、B两个等级,对每种产品,两道工序的加工结果都为A级时,产品为一等品,其余均为二等品