题目内容
某工厂生产甲、乙两种产品.已知生产一吨甲产品、一吨乙产品所需要的煤、电以及产值如表所示;
又知道国家每天分配给该厂的煤和电力有限制,每天供煤至多56吨,供电至多45千瓦.问该厂如何安排生产,才能使该厂日产值最大?最大的产值是多少?
| 用煤(吨) | 用电(千瓦) | 产值(万元) | |
| 生产一吨甲种产品 | 7 | 2 | 8 |
| 生产一吨乙种产品 | 3 | 5 | 11 |
分析:求得线性约束条件
,目标函数为z=8x+11y,作出可行域,根据图象即可求得结论.
|
解答: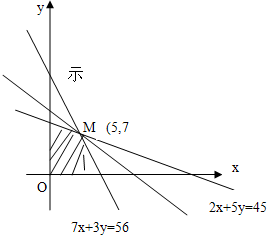 解:设每天生产甲种产品x吨,乙种产品y吨.
解:设每天生产甲种产品x吨,乙种产品y吨.
依题意可得线性约束条件
…(5分)
目标函数为z=8x+11y,…(7分)
作出线性约束条件所表示的平面区域如图所示…(10分)
将z=8x+11y变形为y=-
x+
当直线y=-
x+
在纵轴上的截距
达到最大值时,
即直线y=-
x+
经过点M时,z也达到最大值.
由
得M点的坐标为(5,7)…(12分)
所以当x=5,y=7时,zmax=5×8+7×11=117 …(13分)
因此,该厂每天生产甲种产品5吨,乙种产品7吨,才能使该厂日产值最大,最大的产值是117万元.…(14分)
 解:设每天生产甲种产品x吨,乙种产品y吨.
解:设每天生产甲种产品x吨,乙种产品y吨.依题意可得线性约束条件
|
目标函数为z=8x+11y,…(7分)
作出线性约束条件所表示的平面区域如图所示…(10分)
将z=8x+11y变形为y=-
| 8 |
| 11 |
| z |
| 11 |
当直线y=-
| 8 |
| 11 |
| z |
| 11 |
| z |
| 11 |
即直线y=-
| 8 |
| 11 |
| z |
| 11 |
由
|
所以当x=5,y=7时,zmax=5×8+7×11=117 …(13分)
因此,该厂每天生产甲种产品5吨,乙种产品7吨,才能使该厂日产值最大,最大的产值是117万元.…(14分)
点评:本题考查线性规划知识的运用,考查数形结合的数学思想,考查学生利用数学知识解决实际问题的能力,属于中档题.

练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目
 18、某工厂生产甲、乙两种产品,每种产品都是经过第一道和第二道工序加工而成,两道工序的加工结果相互独立,每道工序的加工结果均有A、B两个等级,对每种产品,两道工序的加工结果都为A级时,产品为一等品,其余均为二等品
18、某工厂生产甲、乙两种产品,每种产品都是经过第一道和第二道工序加工而成,两道工序的加工结果相互独立,每道工序的加工结果均有A、B两个等级,对每种产品,两道工序的加工结果都为A级时,产品为一等品,其余均为二等品