题目内容
(本小题12分) 在某化学实验中,测得如下表所示的6组数据,其中x(min)表示化学反应进行的时,y(mg)表示未转化物质的量
| x(min) | l | 2 | 3 | 4 | 5 | 6 |
| y(mg) | 39.8 | 32.2 | 25.4 | 20.3 | 16.2 | 13.3 |
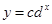 ,试根据测量数据估计c和d的值;
,试根据测量数据估计c和d的值;(2)估计化学反应进行到10 min时未转化物质的量.
(1) c,d的估计值分别为49. 675,0. 801 0.(2)54mg
解析试题分析:(1)在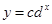 的两边取自然对数,可得lny="ln" c+xlnd,设lny=z,ln c="a," lnd=b,则z=a+bx,由已知数据有
的两边取自然对数,可得lny="ln" c+xlnd,设lny=z,ln c="a," lnd=b,则z=a+bx,由已知数据有
由公式得a≈3.905 5,b≈0. 221 9,线性回归方程为x 1 2 3 4 5 6 y 39.8 32.2 25.4 20.3 16.2 13.3 z 3.684 3.472 3.235 3.011 2.875 2.588 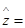 3.9055+ 0.221 9x,
3.9055+ 0.221 9x,
即lnc≈3.905 5,lad≈0.221 9,故c≈49.675,d≈0.801 0,所以c,d的估计值分别为
49. 675,0. 801 0.
(2)54mg
考点:本题主要考查回归分析的概念及思想方法。
点评:典型题,利用所给数据先确定线性回归方程,作出进一步推测。

 名校课堂系列答案
名校课堂系列答案某市居民1999~2003年货币收入 与购买商品支出
与购买商品支出 的统计资料如下表所示:单位:亿元
的统计资料如下表所示:单位:亿元
| 年份 | 1999 | 2000 | 2001 | 2002 | 2003 |
货币收入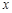 | 40 | 42 | 44 | 47 | 50 |
购买商品支出 | 33 | 34 | 36 | 39 | 41 |

(Ⅱ)已知
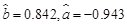 ,请写出Y对x的回归直 线方程,并估计货币收入为52(亿元)时,购买商品支出大致为多少亿元?
,请写出Y对x的回归直 线方程,并估计货币收入为52(亿元)时,购买商品支出大致为多少亿元? 电视传媒公司为了解某地区观众对某类体育节目的收视情况,随机抽取了100名观众进行调查,其中女性有55名。下面是根据调查结果绘制的观众日均收看该体育节目时间的频率分布直方图:
将日均收看该体育节目时间不低于40分钟的观众称为“体育迷”,已知“体育迷”中有10名女性.
(Ⅰ)根据已知条件完成下面的2×2列联表,并据此资料判断是否有95%的把握认为“体育迷”与性别有关?
| | 非体育迷 | 体育迷 | 合计 |
| 男 | | | |
| 女 | | | |
| 合计 | | | |
附:K2=
 ,其中n=a+b+c+d.
,其中n=a+b+c+d.| P(K2≥k) | 0.05 | 0.01 |
| k | 3.841 | 6.635 |
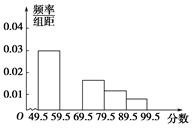
(本题满分10分)对某校高三年级学生参加社区服务次数进行统计,随机抽取 名学生作为样本,得到这
名学生作为样本,得到这 名学生参加社区服务的次数.根据此数据作出了频数与频率的统计表和频率分布直方图如下:
名学生参加社区服务的次数.根据此数据作出了频数与频率的统计表和频率分布直方图如下:
| 分组 | 频数 | 频率 |
 | 10 | 0.25 |
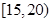 | 24 |  |
 |  |  |
 | 2 | 0.05 |
| 合计 |  | 1 |

(Ⅰ)求出表中
 及图中
及图中 的值;
的值;(Ⅱ)若该校高三学生有240人,试估计该校高三学生参加社区服务的次数在区间
 内的人数;
内的人数;(Ⅲ)在所取样本中,从参加社区服务的次数不少于20次的学生中任选2人,求至多一人参加社区服务次数在区间
 内的概率.
内的概率. (本小题满分10分)国家有甲,乙两个射击队,若两个队共进行了8次热身赛,
各队的总成绩见下表:
| 甲队 | 403 | 390 | 397 | 404 | 388 | 400 | 412 | 406 |
| 乙队 | 417 | 401 | 410 | 416 | 406 | 421 | 398 | 411 |
分别求两个队总成绩的样本平均数和样本方差,根据计算结果,若选一个代表队参加奥运会比赛,你认为应该选哪一个队?
某车间为了规定工时定额,需要确定加个某零件所花费的时间,为此作了四次实验,得到的数据如下:
| 零件的个数x(个) | 2 | 3 | 4 | 5 |
| 加工的时间y(小时) | 2.5 | 3 | 4 | 4.5 |
(2) 试预测加工10个零件需要多少时间?

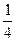 ,且该组中,青年人占50%,中年人占40%,老年人占10%。为了了解各组不同的年龄层次的职工对本次活动的满意程度,现用分层抽样的方法从参加活动的全体职工中抽取一个容量为200的样本。试确定
,且该组中,青年人占50%,中年人占40%,老年人占10%。为了了解各组不同的年龄层次的职工对本次活动的满意程度,现用分层抽样的方法从参加活动的全体职工中抽取一个容量为200的样本。试确定