题目内容
(12分)某单位最近组织了一次健身活动,活动分为登山组和游泳组,且每个职工至多参加了其中一组。在参加活动的职工中,青年人占42.5%,中年人占47.5%,老年人占10%。登山组的职工占参加活动总人数的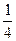 ,且该组中,青年人占50%,中年人占40%,老年人占10%。为了了解各组不同的年龄层次的职工对本次活动的满意程度,现用分层抽样的方法从参加活动的全体职工中抽取一个容量为200的样本。试确定
,且该组中,青年人占50%,中年人占40%,老年人占10%。为了了解各组不同的年龄层次的职工对本次活动的满意程度,现用分层抽样的方法从参加活动的全体职工中抽取一个容量为200的样本。试确定
(Ⅰ)游泳组中,青年人、中年人、老年人分别所占的比例;
(Ⅱ)游泳组中,青年人、中年人、老年人分别应抽取的人数。
解:(Ⅰ)设登山组人数为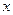 ,游泳组中,青年人、中年人、老年人各占比例分别为a、b、c,则有
,游泳组中,青年人、中年人、老年人各占比例分别为a、b、c,则有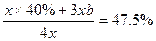 ,
,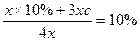 ,解得b=50%,c=10%.
,解得b=50%,c=10%.
故a=100%-50%-10%=40%,即游泳组中,青年人、中年人、老年人各占比例分别为40%、
50%、10%。
(Ⅱ)游泳组中,抽取的青年人数为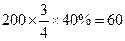 (人);
(人);
抽取的中年人数为 50%=75(人);
50%=75(人);
抽取的老年人数为 10%=15(人)。
10%=15(人)。
解析

 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案 (本小题12分) 在某化学实验中,测得如下表所示的6组数据,其中x(min)表示化学反应进行的时,y(mg)表示未转化物质的量
| x(min) | l | 2 | 3 | 4 | 5 | 6 |
| y(mg) | 39.8 | 32.2 | 25.4 | 20.3 | 16.2 | 13.3 |
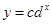 ,试根据测量数据估计c和d的值;
,试根据测量数据估计c和d的值;(2)估计化学反应进行到10 min时未转化物质的量.
为了参加奥运会,对自行车运动员甲、乙两人在相同的条件下进行了6次测试,测得他们的最大速度的数据如表所示:请判断:谁参加这项重大比赛更合适,并阐述理由。
| 甲 | 27 | 38 | 30 | 37 | 35 | 31 |
| 乙 | 33 | 29 | 38 | 34 | 28 | 36 |
(本题满分12分)对甲、乙两名自行车赛手在相同条件下进行了6次测试,测得
他们的最大速度(m/s)的数据如下表.
| 甲 | 27 | 38 | 30 | 37 | 35 | 31 |
| 乙 | 33 | 29 | 38 | 34 | 28 | 36 |
(1)画出茎叶图
(2)分别求出甲、乙两名自行车赛手最大速度(m/s)数据的平均数、中位数、标准差,并判断选谁参加比赛更合适.
某科研部门现有男技术员45人,女技术员15人,为研发某新产品的需要,科研部门按照分层抽样的方法组建了一个由四人组成的新产品研发小组.
(1)求每一个技术员被抽到的概率及该新产品研发小组中男、女技术员的人数;
(2)一年后研发小组决定选两名研发的技术员对该项研发产品进行检验,方法是先从研发小组中选一人进行检验,该技术员检验结束后,再从研发小组内剩下的三名技术员中选一人进行检验,若两名技术员检验得到的数据如下:
| 第一次被抽到进行检验的技术员 | 58 | 53 | 87 | 62 | 78 | 70 | 82 |
| 第二次被抽到进行检验的技术员 | 64 | 61 | 78 | 66 | 74 | 71 | 76 |
② 请问哪位技术员检验更稳定?并说明理由.
(12分)假设关于某市房屋面积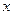 (平方米)与购房费用
(平方米)与购房费用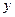 (万元),有如下的统计数据:
(万元),有如下的统计数据:
| x(平方米) | 80 | 90 | 100 | 110 |
| y(万元) | 42 | 46 | 53 | 59 |
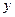 对
对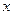 呈线性相关。
呈线性相关。(1)求回归直线方程;
(2)若在该市购买120平方米的房屋,估计购房费用是多少?
公式:
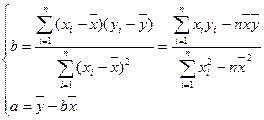
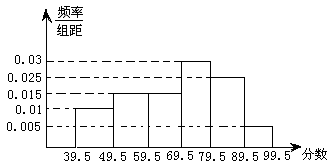

 高度大约是多少?(计算时可以用组中值代替各组数据的平均值);
高度大约是多少?(计算时可以用组中值代替各组数据的平均值); 组中移出一棵树苗,从
组中移出一棵树苗,从 组中移出两棵树苗进行试验研究,则
组中移出两棵树苗进行试验研究,则