题目内容
(本小题共13分)
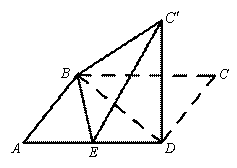
已知平行四边形ABCD中,AB=6,AD=10,BD=8,E是线段AD的中点.沿BD将△BCD翻折到△![]() ,使得平面
,使得平面![]() ⊥平面ABD.
⊥平面ABD.
 (Ⅰ)求证:
(Ⅰ)求证:![]() 平面ABD;
平面ABD;
(Ⅱ)求直线![]() 与平面
与平面![]() 所成角的正弦值;
所成角的正弦值;
(Ⅲ)求二面角![]() 的余弦值.
的余弦值.
(本小题共13分)
证明:(Ⅰ)平行四边形ABCD中,AB=6,AD=10,BD=8,
沿直线BD将△BCD翻折成△![]()
可知CD=6,BC’=BC=10,BD=8,
即![]() ,
,
故![]() . ………………2分
. ………………2分
∵平面![]() ⊥平面
⊥平面![]() ,平面
,平面![]()
![]() 平面
平面![]() =
=![]() ,
,![]() 平面
平面![]() ,
,
∴![]() 平面
平面![]() . ………………5分
. ………………5分
(Ⅱ)由(Ⅰ)知![]() 平面ABD,且
平面ABD,且![]() ,
,
如图,以D为原点,建立空间直角坐标系![]() . ………………6分
. ………………6分
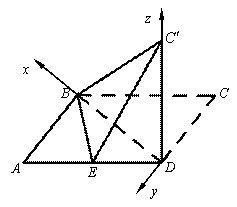 则
则![]() ,
,![]() ,
,![]() ,
,![]() .
.
∵E是线段AD的中点,
∴![]() ,
,![]() .
.
在平面![]() 中,
中,![]() ,
,![]() ,
,
设平面![]() 法向量为
法向量为![]() ,
,
∴ 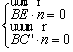 ,即
,即![]() ,
,
令![]() ,得
,得![]() ,故
,故![]() . ………………8分
. ………………8分
设直线![]() 与平面
与平面![]() 所成角为
所成角为![]() ,则
,则
![]() . ………………9分
. ………………9分
∴ 直线![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() . ………………10分
. ………………10分
(Ⅲ)由(Ⅱ)知平面![]() 的法向量为
的法向量为![]() ,
,
而平面![]() 的法向量为
的法向量为![]() ,
,
∴ ![]() ,
,
因为二面角![]() 为锐角,
为锐角,
所以二面角![]() 的余弦值为
的余弦值为![]() . ………………13分
. ………………13分

练习册系列答案
 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案
相关题目
 .
. 在
在 处取得极值,求a的值;
处取得极值,求a的值; 在
在 上的最大值.
上的最大值. ,设函数
,设函数 .
. 在
在 上的单调递增区间;
上的单调递增区间; 中,
中, ,
, ,
, 分别是角
分别是角 ,
, ,
, 的对边,
的对边, ,
, ,
, ,求边
,求边 ,求
,求
 的最小正周期及图象的对称轴方程式;
的最小正周期及图象的对称轴方程式; 的条件下,求
的条件下,求 的值.
的值.