题目内容
已知二次函数f(x)=ax2+x.
(1)设函数g(x)=(1-2t)x+t2-1,当a=1,函数h(x)=f(x)+g(x)在区间(-2,4)内有两个相异的零点,求实数t的取值范围.
(2)当a>0,求证对任意两个不等的实数x1,x2,都有 ;
;
(3)若x∈[0,1]时,-1≤f(x)≤1,求实数a的取值范围.
解:(1)当a=1,函数h(x)=f(x)+g(x)=x2+(2-2t)x+t2-1.
由题意可得 ,即
,即 ,解得-2+
,解得-2+ <t<1.
<t<1.
故实数t的取值范围为(-2+ ,1).
,1).
(2)∵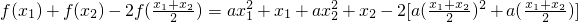
= ,
,
故对任意两个不等的实数x1,x2,都有 .
.
(3)由题意可得x∈[0,1]时,-1≤f(x)≤1,即-1≤ax2+x≤1,
即x∈[0,1]时,ax2+x+1≥0且ax2+x-1≤0恒成立,
当x=0时,显然,ax2+x+1≥0且ax2+x-1≤0均成立.
当x∈(0,1]时,由ax2+x+1≥0恒成立,得 ,
,
而 在x∈(0,1]最大值为-2,∴a≥-2.
在x∈(0,1]最大值为-2,∴a≥-2.
当x∈(0,1]时,由ax2+x-1≤0恒成立,得 ,
,
而 在x∈(0,1]最小值为0,∴a≤0.
在x∈(0,1]最小值为0,∴a≤0.
综上可得,-2≤a≤0.
而由题意可得a≠0,因此所求的a的取值范围为[-2,0).
分析:(1)当a=1,函数h(x)=x2+(2-2t)x+t2-1,由题意可得 ,由此求得实数t的取值范围
,由此求得实数t的取值范围
(2)计算 ,化简可得
,化简可得  ,从而证得结论.
,从而证得结论.
(3)由题意可得x∈[0,1]时,-1≤ax2+x≤1,当x=0时,显然成立.当x∈(0,1]时,由ax2+x+1≥0恒成立,求得a≥-2;由ax2+x-1≤0恒成立,求得a≤0.再由a不等于0,从而求得a的取值范围.
点评:本题主要考查了一元二次方程的根的分布与系数的关系,二次函数的性质的应用,函数的恒成立问题,属于中档题.
由题意可得
 ,即
,即 ,解得-2+
,解得-2+ <t<1.
<t<1.故实数t的取值范围为(-2+
 ,1).
,1).(2)∵
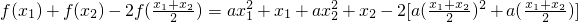
=
 ,
,故对任意两个不等的实数x1,x2,都有
 .
.(3)由题意可得x∈[0,1]时,-1≤f(x)≤1,即-1≤ax2+x≤1,
即x∈[0,1]时,ax2+x+1≥0且ax2+x-1≤0恒成立,
当x=0时,显然,ax2+x+1≥0且ax2+x-1≤0均成立.
当x∈(0,1]时,由ax2+x+1≥0恒成立,得
 ,
,而
 在x∈(0,1]最大值为-2,∴a≥-2.
在x∈(0,1]最大值为-2,∴a≥-2.当x∈(0,1]时,由ax2+x-1≤0恒成立,得
 ,
,而
 在x∈(0,1]最小值为0,∴a≤0.
在x∈(0,1]最小值为0,∴a≤0.综上可得,-2≤a≤0.
而由题意可得a≠0,因此所求的a的取值范围为[-2,0).
分析:(1)当a=1,函数h(x)=x2+(2-2t)x+t2-1,由题意可得
 ,由此求得实数t的取值范围
,由此求得实数t的取值范围(2)计算
 ,化简可得
,化简可得  ,从而证得结论.
,从而证得结论.(3)由题意可得x∈[0,1]时,-1≤ax2+x≤1,当x=0时,显然成立.当x∈(0,1]时,由ax2+x+1≥0恒成立,求得a≥-2;由ax2+x-1≤0恒成立,求得a≤0.再由a不等于0,从而求得a的取值范围.
点评:本题主要考查了一元二次方程的根的分布与系数的关系,二次函数的性质的应用,函数的恒成立问题,属于中档题.

练习册系列答案
 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案
相关题目