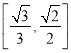题目内容
【题目】在平面直角坐标系
中，直线
的参数方程是：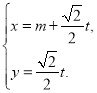
（
是参数）.以原点
为极点，x轴的正半轴为极轴建立极坐标系，曲线
的极坐标方程是
.
（1）若直线与曲线相交于
两点，且
，试求实数
值；
（2）设
为曲线上任意一点，求
的取值范围.
【答案】（1）
或
；（2）
.
【解析】
（1）把直线、曲线方程化为直角坐标方程后根据圆心到直线的距离和半径的关系建立方程即可．（2）利用圆的参数方程，根据点到直线的距离公式和三角函数的知识求解．
解析：（1）曲线
的极坐标方程是
化为直角坐标方程为：
，直线
的直角坐标方程为：
.
所以圆心
到直线的距离（弦心距）
，
圆心到直线的距离为：
，
所以
所以或，
（2）曲线C的方程可化为
，其参数方程为
（
为参数）
因为
为曲线C上任意一点，
所以
的取值范围是.
练习册系列答案
相关题目
【题目】已知椭圆
的焦点在
轴上，中心在坐标原点，抛物线
的焦点在
轴上，顶点在坐标原点，在、上各取两个点，将其坐标记录于表格中：
|
|
|
|
|
|
|
|
|
|
（1）求、的标准方程；
（2）已知定点
，
为抛物线上的一动点，过点
作抛物线的切线交椭圆于
、
两点，求
面积的最大值．
