Question

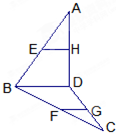已知E、F、G、H是所在线段上的点，且EH∥FG．
求证：EH∥BD．

Answer 1

分析：根据一条直线在平面上，一条直线与这条直线平行，根据这两个条件得到直线与平面平行，根据线与面平行的性质，得到线与线平行，得到结论．

解答：证明：∵点E、F、G、H为空间四边形边AB、BC、CD、DA上的点
∴直线EH?平面BCD，直线FG?平面BCD
又EH∥FG
∴直线EH∥平面BCD
又∵EH?平面ABD且平面ABD∩平面BCD=BD
∴EH∥BD

点评：本题考查线与面平行的判断，线与面平行的性质，考查线面平行的判定和性质的综合应用，本题是一个考查知识点比较集中的题目，只考线与面的平行，是一个目标很明确的题目．