题目内容
5、已知E,F,G,H是空间四点,命题甲:E,F,G,H四点不共面,命题乙:直线EF和GH不相交,则甲是乙成立的( )
分析:利用公理2可知四点不共面,则由它们确定的直线一定不相交,通过条件的判断,可知甲是乙的充分不必要条件.
解答:解:∵E,F,G,H是空间四点且不共面∴直线EF和GH不相交∴甲?乙
若直线EF和GH不相交,则它们可能平行,∴E,F,G,H四点共面,∴乙推不出甲
故甲是乙成立的充分不必要条件
故选A.
若直线EF和GH不相交,则它们可能平行,∴E,F,G,H四点共面,∴乙推不出甲
故甲是乙成立的充分不必要条件
故选A.
点评:本题主要考查了空间中点,线,面的位置关系,同时考查了必要条件,充分条件与冲要条件的判断,基本的定理和定义是解决问题的通法,是个基础题.

练习册系列答案
 智能训练练测考系列答案
智能训练练测考系列答案 计算高手系列答案
计算高手系列答案
相关题目
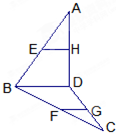 已知E、F、G、H是所在线段上的点,且EH∥FG.
已知E、F、G、H是所在线段上的点,且EH∥FG.