题目内容
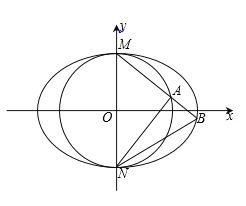
【题目】已知双曲线 C 经过点 (2,3),它的渐近线方程为 y = ±![]() .椭圆 C1与双曲线 C有相同的焦点,椭圆 C1的短轴长与双曲线 C 的实轴长相等.
.椭圆 C1与双曲线 C有相同的焦点,椭圆 C1的短轴长与双曲线 C 的实轴长相等.
(1)求双曲线 C 和椭圆 C1 的方程;
(2)经过椭圆 C1 左焦点 F 的直线 l 与椭圆 C1 交于 A、B 两点,是否存在定点 D ,使得无论 AB 怎样运动,都有∠ADF = ∠BDF ?若存在,求出 D 点坐标;若不存在,请说明理由.
【答案】(1)![]() ;
;![]() (2)存在点D
(2)存在点D ![]()
【解析】
(1)双曲线![]() 的方程为:
的方程为:![]() ,则
,则![]() .设椭圆
.设椭圆![]() 的方程;
的方程;![]() 椭圆
椭圆![]() 的短轴长与双曲线
的短轴长与双曲线![]() 的实轴长相等,椭圆
的实轴长相等,椭圆![]() 与双曲线
与双曲线![]() 有相同的焦点
有相同的焦点![]() 即可得
即可得![]() 、
、![]() 、
、![]()
(2)直线![]() 垂直
垂直![]() 轴时,
轴时,![]() 、
、![]() 两点关于
两点关于![]() 轴对称,要使
轴对称,要使![]() ,则点
,则点![]() 必在
必在![]() 轴上,设
轴上,设![]() ,直线
,直线![]() 不垂直
不垂直![]() 轴时,
轴时,![]() 的方程设为:
的方程设为:![]() ,设
,设![]() ,
,![]() ,
,![]() ,
,![]() ,联立
,联立![]() 得
得![]() .要使
.要使![]() ,即直线
,即直线![]() 、
、![]() 的斜率互为相反数,即
的斜率互为相反数,即![]() ,求得
,求得![]()
解:(1)双曲线![]() 方程为:
方程为:![]() ,则
,则![]() .
.
![]() 双曲线
双曲线![]() 的方程为
的方程为![]() .
.
设椭圆![]() 的方程;
的方程;![]()
椭圆![]() 的短轴长与双曲线
的短轴长与双曲线![]() 的实轴长相等,
的实轴长相等,
![]() 椭圆
椭圆![]() 的短轴长为
的短轴长为![]() ,椭圆
,椭圆![]() 与双曲线
与双曲线![]() 有相同的焦点
有相同的焦点![]() ,
,
即![]() ,
,![]() ,椭圆
,椭圆![]() 的方程为:
的方程为:![]() ;
;
(2)直线![]() 垂直
垂直![]() 轴时,
轴时,![]() 、
、![]() 两点关于
两点关于![]() 轴对称,
轴对称,
![]() ,
,![]() 要使
要使![]() ,则点
,则点![]() 必在
必在![]() 轴上,
轴上,
设![]() ,直线
,直线![]() 不垂直
不垂直![]() 轴时,
轴时,![]() 的方程设为:
的方程设为:![]() ,
,
设![]() ,
,![]() ,
,![]() ,
,![]() ,联立
,联立![]() 得
得![]() .
.
![]()
![]() .
.
![]() ,
,![]() 直线
直线![]() 、
、![]() 的斜率互为相反数,
的斜率互为相反数,
即![]() ,
,
![]() 时恒成立.
时恒成立.
![]() 时,
时,![]() ;
;
![]() 存在定点
存在定点![]() ,
,![]() ,使得无论
,使得无论![]() 怎样运动,都有
怎样运动,都有![]() .
.

练习册系列答案
相关题目