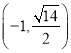题目内容
【题目】设函数![]() (a,b
(a,b![]() R).
R).
(1)当b=﹣1时,函数![]() 有两个极值,求a的取值范围;
有两个极值,求a的取值范围;
(2)当a+b=1时,函数![]() 的最小值为2,求a的值;
的最小值为2,求a的值;
(3)对任意给定的正实数a,b,证明:存在实数![]() ,当
,当![]() 时,
时,![]() .
.
【答案】(1)(![]() ,0)(2)
,0)(2)![]() 或
或![]() (3)证明见解析;
(3)证明见解析;
【解析】
(1)当![]() 时,
时,![]() ,求导
,求导![]() ,则
,则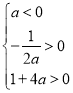 ,解出即可;
,解出即可;
(2)当![]() 时,
时,![]() ,求导后,分类讨论得函数的单调性与最值,由此可求出答案;
,求导后,分类讨论得函数的单调性与最值,由此可求出答案;
(3)对任意给定的正实数a,b,有![]() ,设
,设![]() ,设
,设![]() ,x>0,求导后易求得
,x>0,求导后易求得![]() ,又由
,又由![]() ,得
,得![]() ,由此可得出答案.
,由此可得出答案.
解:(1)当![]() 时,
时,![]() ,
,
∴![]() ,
,
若函数![]() 有两个极值,则
有两个极值,则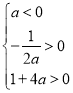 ,解得
,解得![]() ,
,
故a的取值范围是(![]() ,0);
,0);
(2)当![]() 时,
时,![]() ,
,
∴![]() ,
,
当a≤0时,![]() ,∴
,∴![]() 是(0,
是(0,![]() )上的减函数,
)上的减函数,
∴函数![]() 无最小值,舍去;
无最小值,舍去;
当a>0时,由![]() 得,
得,![]() ,
,
∴![]() 在(0,
在(0,![]() )上单调递减,在(
)上单调递减,在(![]() ,
,![]() )上单调递增,
)上单调递增,
∴函数![]() 的最小值为
的最小值为![]() ,
,
由![]() ,得
,得![]() ,
,
解得![]() 或
或![]() ;
;
(3)对任意给定的正实数a,b,有![]() ,
,
设![]() ,
,
设![]() ,x>0,则
,x>0,则![]() ,z
,z
易知当x=4时,![]() ,故
,故![]() ,
,
又由![]() ,得
,得![]() ,
,
对于任意给定的正实数a,b,取![]() 为
为![]() 与4中的较大者,
与4中的较大者,
则当![]() 时,恒有
时,恒有![]() ,即当
,即当![]() 时,
时,![]() .
.

 提分百分百检测卷系列答案
提分百分百检测卷系列答案【题目】为了提高生产线的运行效率,工厂对生产线的设备进行了技术改造.为了对比技术改造后的效果,采集了生产线的技术改造前后各![]() 次连续正常运行的时间长度(单位:天)数据,并绘制了如茎叶图:
次连续正常运行的时间长度(单位:天)数据,并绘制了如茎叶图:
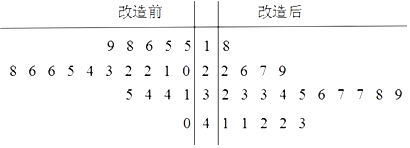
(1)①设所采集的![]() 个连续正常运行时间的中位数
个连续正常运行时间的中位数![]() ,并将连续正常运行时间超过
,并将连续正常运行时间超过![]() 和不超过
和不超过![]() 的次数填入下面的列联表:
的次数填入下面的列联表:
超过 | 不超过 | |
改造前 |
|
|
改造后 |
|
|
②根据①中的列联表,能否有![]() 的把握认为生产线技术改造前后的连续正常运行时间有差异?
的把握认为生产线技术改造前后的连续正常运行时间有差异?
附: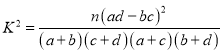 .
.
|
|
|
|
|
|
|
|
(2)工厂的生产线的运行需要进行维护,工厂对生产线的生产维护费用包括正常维护费、保障维护费两种.对生产线设定维护周期为![]() 天(即从开工运行到第
天(即从开工运行到第![]() 天
天![]() 进行维护.生产线在一个生产周期内设置几个维护周期,每个维护周期相互独立.在一个维护周期内,若生产线能连续运行,则不会产生保障维护费;若生产线不能连续运行,则产生保障维护费.经测算,正常维护费为
进行维护.生产线在一个生产周期内设置几个维护周期,每个维护周期相互独立.在一个维护周期内,若生产线能连续运行,则不会产生保障维护费;若生产线不能连续运行,则产生保障维护费.经测算,正常维护费为![]() 万元/次;保障维护费第一次为
万元/次;保障维护费第一次为![]() 万元/周期,此后每增加一次则保障维护费增加
万元/周期,此后每增加一次则保障维护费增加![]() 万元.现制定生产线一个生产周期(以
万元.现制定生产线一个生产周期(以![]() 天计)内的维护方案:
天计)内的维护方案:![]() ,
,![]() 、
、![]() 、
、![]() 、
、![]() .以生产线在技术改造后一个维护周期内能连续正常运行的频率作为概率,求一个生产周期内生产维护费的分布列及期望值.
.以生产线在技术改造后一个维护周期内能连续正常运行的频率作为概率,求一个生产周期内生产维护费的分布列及期望值.