题目内容
(本小题12分)设函数f(x)=a·b,其中a=(2cosx,1), b=(cosx,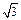 sin2x), x∈R.
sin2x), x∈R.
(1)若f(x)=1-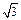 ,且x∈[
,且x∈[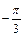 ,
,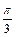 ],求x;
],求x;
(2)若函数y=2sin2x的图象按向量c=(m,n)(|m|<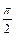 )平移后得到函数y= f(x)的图象,求实数m、n的值.
)平移后得到函数y= f(x)的图象,求实数m、n的值.
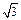 sin2x), x∈R.
sin2x), x∈R.(1)若f(x)=1-
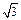 ,且x∈[
,且x∈[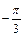 ,
,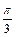 ],求x;
],求x;(2)若函数y=2sin2x的图象按向量c=(m,n)(|m|<
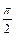 )平移后得到函数y= f(x)的图象,求实数m、n的值.
)平移后得到函数y= f(x)的图象,求实数m、n的值.(1) f(x)=a·b=1+2sin(2x+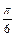 ),由1+2sin(2x+
),由1+2sin(2x+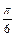 )=1-
)=1-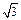 ,得sin(2x+
,得sin(2x+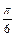 )=-
)=-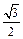 ,
,
∵x∈[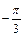 ,
,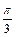 ],∴
],∴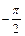 ≤2x+
≤2x+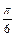 ≤
≤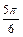 .∴2x+
.∴2x+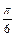 =
=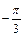 ,即x=
,即x=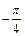 .
.
(2)函数y=2sin2x的图象按向量c=(m,n) 平移后得到函数y=2sin2(x-m)+n的图象,即函数y= f(x)的图象.由(1)得f(x)= 2sin2(x+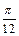 )+ 1, ∵|m|<
)+ 1, ∵|m|<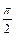 ,∴m= -
,∴m= -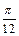 ,n=1.
,n=1.
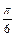 ),由1+2sin(2x+
),由1+2sin(2x+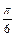 )=1-
)=1-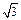 ,得sin(2x+
,得sin(2x+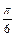 )=-
)=-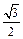 ,
,∵x∈[
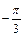 ,
,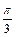 ],∴
],∴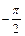 ≤2x+
≤2x+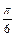 ≤
≤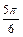 .∴2x+
.∴2x+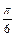 =
=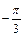 ,即x=
,即x=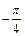 .
.(2)函数y=2sin2x的图象按向量c=(m,n) 平移后得到函数y=2sin2(x-m)+n的图象,即函数y= f(x)的图象.由(1)得f(x)= 2sin2(x+
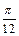 )+ 1, ∵|m|<
)+ 1, ∵|m|<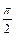 ,∴m= -
,∴m= -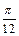 ,n=1.
,n=1.略

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
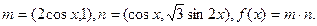
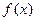 的最小正周期和最大值;
的最小正周期和最大值;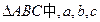 分别是角A、B、C的对边,且
分别是角A、B、C的对边,且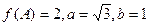 ,求角C。
,求角C。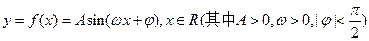 的图象在
的图象在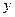 轴右侧的第一个最值点(最
轴右侧的第一个最值点(最 高点或最低点)为
高点或最低点)为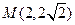 ,与
,与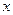 轴在原点左侧的第一个交点为N
轴在原点左侧的第一个交点为N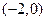 .
.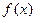 的图象在M,N之间与
的图象在M,N之间与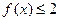 .
.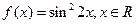 ,则
,则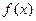 是( )
是( )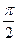 的偶函数
的偶函数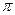 的偶函数
的偶函数
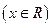 ,有下列四个命题:(1)由
,有下列四个命题:(1)由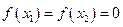 可得
可得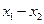 必是
必是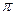 的整数倍;(2)
的整数倍;(2)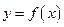 的表达式可改写为
的表达式可改写为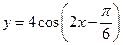 ;(3)
;(3)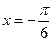 对称;(4)
对称;(4)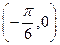 对称,其中正确的是 (填序号)
对称,其中正确的是 (填序号)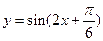 的图像向左平移
的图像向左平移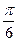 个单位,所得图像的函数解析式为( )
个单位,所得图像的函数解析式为( )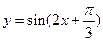
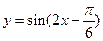
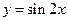
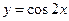
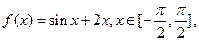 且
且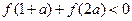 ,则
,则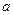 的取值范围是
的取值范围是 
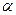 ,使
,使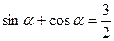
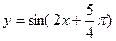 +1的一个对称中心为
+1的一个对称中心为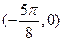
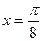 是函数
是函数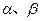 是第一象限的角,且
是第一象限的角,且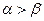 ,则
,则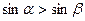
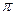 的是(★)
的是(★)


