题目内容
13．已知一次函数f（x）=ax+b，满足f（2）=0，f（-2）=1，则f（4）=（ ）| A． | $\sqrt{2}$ | B． | $\frac{1}{2}$ | C． | -$\frac{1}{2}$ | D． | 1 |
分析 利用已知条件求出函数的解析式，然后求解函数值．
解答 解：一次函数f（x）=ax+b，满足f（2）=0，f（-2）=1，
可得：$\left\{\begin{array}{l}2a+b=0\\-2a+b=1\end{array}\right.$，解得b=$\frac{1}{2}$，a=$-\frac{1}{4}$．
一次函数f（x）=-$\frac{1}{4}$x+$\frac{1}{2}$，
f（4）=-1+$\frac{1}{2}$=-$\frac{1}{2}$．
故选：C．
点评 本题考查函数的解析式的求法，函数值的求法，考查计算能力．
练习册系列答案
相关题目
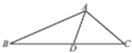如图，在△ABC中，AB=3，AC=2，BC=4，点D在边BC上，∠BAD=30°，则sin∠CAD的值为$\frac{3\sqrt{5}+1}{8}$．