题目内容
已知数列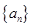 中,
中,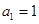 ,
, ,数列
,数列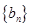 中,
中, ,且点
,且点 在直线
在直线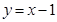 上.
上.
(Ⅰ)求数列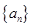 的通项公式;
的通项公式;
(Ⅱ)求数列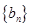 的通项公式;
的通项公式;
(Ⅲ)若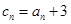 ,求数列
,求数列 的前项和
的前项和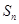 .
.
(Ⅰ) 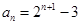 ;(Ⅱ)
;(Ⅱ)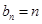 ;(Ⅲ)
;(Ⅲ)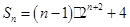 .
.
解析试题分析:(Ⅰ) 由已知可构造数列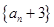 ,并证明其为等比数列,先求出数列
,并证明其为等比数列,先求出数列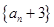 的通项公式,再求数列
的通项公式,再求数列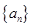 的通项公式(一般形如
的通项公式(一般形如 的递推关系,可先构造等比数列
的递推关系,可先构造等比数列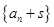 ,其公比
,其公比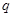 与常数
与常数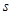 ,可由
,可由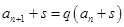 与所给等式
与所给等式 进行比较求得);(Ⅱ)将点
进行比较求得);(Ⅱ)将点 代入直线方程
代入直线方程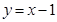 ,可得到数列
,可得到数列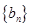 中
中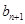 与
与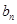 的关系式,从而发现
的关系式,从而发现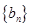 为等差数列,即可求出数列
为等差数列,即可求出数列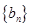 的通项公式;(Ⅲ)由(Ⅰ) (Ⅱ)可得数列
的通项公式;(Ⅲ)由(Ⅰ) (Ⅱ)可得数列 的通项公式,观察
的通项公式,观察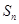 中各项关系,可用错位相减法来求出
中各项关系,可用错位相减法来求出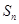 (错位相减法是求数列前项
(错位相减法是求数列前项 和的常用方法,它适用于如果一个数列的各项是由一个等差数列和一个等比数列的对应各项之积构成的).
和的常用方法,它适用于如果一个数列的各项是由一个等差数列和一个等比数列的对应各项之积构成的).
试题解析:(Ⅰ)由 得
得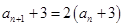
所以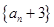 是首项为
是首项为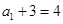 ,公比为2的等比数列.
,公比为2的等比数列.
所以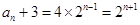 ,故
,故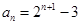
(Ⅱ)因为 在直线
在直线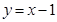 上,
上,
所以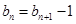 即
即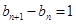 又
又
故数列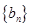 是首项为1,公差为1的等差数列,
是首项为1,公差为1的等差数列,
所以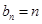
(Ⅲ)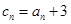 =
=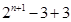 =
=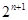 故
故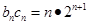
所以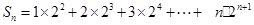
故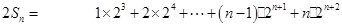
相减得
所以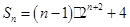
考点:1.等比数列;2.等差数列;3.数列前项 和求法.
和求法.

练习册系列答案
相关题目
 0的等差数列,且它的第2、3、6项依次构成等比数列{bn}的前3项。
0的等差数列,且它的第2、3、6项依次构成等比数列{bn}的前3项。 年,普通型汽车的总耗资费
年,普通型汽车的总耗资费 (万元)的表达式
(万元)的表达式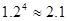
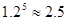
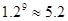
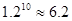 )
)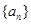 的前6项和为60,且
的前6项和为60,且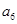 为
为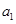 和
和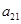 的等比中项.
的等比中项. 满足
满足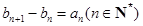 ,且
,且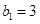 ,求数列
,求数列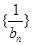 的前
的前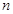 项和
项和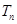 .
.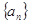 中,
中,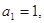 且点
且点 在直线
在直线 上。
上。 的通项公式;
的通项公式;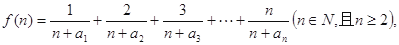 求函数
求函数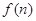 的最小值;
的最小值; 表示数列
表示数列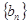 的前项和.试问:是否存在关于
的前项和.试问:是否存在关于 的整式
的整式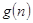 ,使得
,使得 对于一切不小于2的自然数
对于一切不小于2的自然数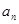 }中,
}中, ,公比
,公比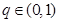 ,且
,且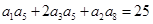 ,
,  与
与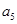 的等比中项为2.
的等比中项为2.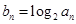 ,求:数列{
,求:数列{ }的前
}的前 项和为
项和为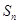 ,
, ,
, ,
,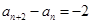
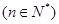
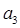

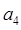 ,并求数列{an}通项公式;
,并求数列{an}通项公式; ,当
,当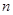 的值.
的值.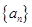 的公差
的公差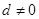 ,它的前
,它的前 项和为
项和为 ,若
,若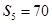 ,且
,且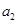 、
、 、
、 成等比数列.
成等比数列. 的前
的前 ,求证:
,求证: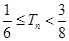 .
. 满足:
满足: ,
, .
. 及
及 的第n项为
的第n项为 ,若
,若 成等差数列,且
成等差数列,且 ,设数列
,设数列 的前
的前 项和
项和 .求数列
.求数列